已知函数f(x)=a+bx-1的图象经过点A(1.3).函数f-1(x+a)的图象经过点B(4,2),试求f-1(x)的表达式. 题目和参考答案——青夏教育精英家教网——

题目内容

已知函数f(x)=a+b^x-1(b＞0,b≠1)的图象经过点A（1，3），函数f^-1(x+a)的图象经过点B(4,2),试求f^-1(x)的表达式.

解析：由y=a+b^x-1(b＞0,b≠1),得x-1=log_b(y-a).

∵b^x-1＞0,则a+b^x-1＞a.

∴y＞a,

∴f^-1(x)=1+log_b(x-a)(x＞a).

∴f^-1(x+a)=1+log_bx(x＞0).

∵点A在f(x)的图象上，点B在f^-1(x+a)的图象上，

∴

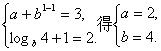
∴f^-1(x)的表达式为f^-1(x)=log₄(x-2)+1(x＞2).

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

已知函数f(x)=a-

．
（1）求证：不论a为何实数f（x）总是为增函数；
（2）确定a的值，使f（x）为奇函数；
（3）当f（x）为奇函数时，求f（x）的值域．

已知函数f(x)

(x-5)2-a，x＞3

（a＞0且a≠1）图象经过点Q（8，6）．
（1）求a的值，并在直线坐标系中画出函数f（x）的大致图象；
（2）求函数f（t）-9的零点；
（3）设q（t）=f（t+1）-f（t）（t∈R），求函数q（t）的单调递增区间．

已知函数f(x)=a-

，若f（x）为奇函数，则a=（　　）

已知函数f(x)=

，其中a＞0．
（I）求函数f（x）的单调区间；
（II）若直线x-y-1=0是曲线y=f（x）的切线，求实数a的值；
（III）设g（x）=xlnx-x²f（x），求g（x）在区间[1，e]上的最小值．（其中e为自然对数的底数）

已知函数f(x)=a-

，（a∈R）
（1）求f（x）的定义域；
（2）若f（x）为奇函数，求a的值；
（3）考察f（x）在定义域上单调性的情况，并证明你的结论．