题目内容
(本小题满分13分)
袋中有大小相同的三个球,编号分别为1、2和3,从袋中每次取出一个球,若取到的球的编号为偶数,则把该球编号加1(如:取到球的编号为2,改为3)后放回袋中继续取球;若取到球的编号为奇数,则取球停止,用 表示所有被取球的编号之和.
表示所有被取球的编号之和.
(Ⅰ)求 的概率分布;
的概率分布;
(Ⅱ)求 的数学期望与方差.
的数学期望与方差.
(1)
(2)
1 3 5 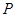

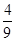
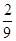
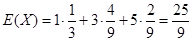
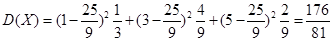 .
.
解析试题分析:解:(Ⅰ)在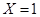 时,表示第一次取到的1号球,
时,表示第一次取到的1号球,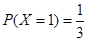 ; 1分
; 1分
在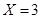 时,表示第一次取到2号球,第二次取到1号球,或第一次取到3号球,
时,表示第一次取到2号球,第二次取到1号球,或第一次取到3号球,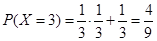 ; 4分
; 4分
在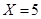 时,表示第一次取到2号球,第二次取到3号球,
时,表示第一次取到2号球,第二次取到3号球,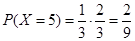 . 6分
. 6分 的概率分布为 7分
的概率分布为 7分
(Ⅱ)
1 3 5 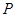

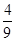
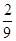
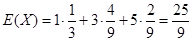 , 10分
, 10分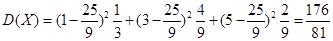 . 13分
. 13分
考点:概率分布列和期望
点评:解决的关键是对于各个取值的概率的准确求解,属于基础题。

练习册系列答案
相关题目
一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个)。按样式分层抽样的方法在这个月生产的灯泡中抽取100个,其中有A样式灯泡25个.
| 型号 | A样式 | B样式 | C样式 |
| 10W | 2000 | z | 3000 |
| 30W | 3000 | 4500 | 5000 |
(1)求z的值;
(2)用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本,从这个样本中任取2个灯泡,求至少有1个10W的概率.
 ,求随机变量
,求随机变量
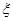 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求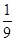 ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为 ,试写出
,试写出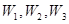 ,物理、化学、生物获得等级不是A的事件分别记为
,物理、化学、生物获得等级不是A的事件分别记为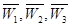 .
.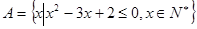 ,集合
,集合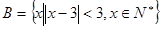 ,
,
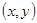 所有可能的结果;
所有可能的结果;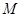 中任取一个元素,求“
中任取一个元素,求“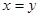 ”的概率
”的概率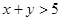 ”的概率.
”的概率.