题目内容
已知矩形ABCD的对角线交于点P(2,0),边AB所在直线的方程为x-3y-6=0,点(-1,1)在边AD所在的直线上,
(1)求矩形ABCD的外接圆的方程;
(2)已知直线l:(1-2k)x+(1+k)y-5+4k=0(k∈R),求证:直线l与矩形ABCD的外接圆恒相交,并求出相交的弦长最短时的直线l的方程.
(1)求矩形ABCD的外接圆的方程;
(2)已知直线l:(1-2k)x+(1+k)y-5+4k=0(k∈R),求证:直线l与矩形ABCD的外接圆恒相交,并求出相交的弦长最短时的直线l的方程.
分析:(1)由lAB:x-3y-6=0且AD⊥AB,点(-1,1)在边AD所在的直线上,得到AD所在直线的方程是:y-1=-3(x+1)即3x+y+2=0,求出交点的坐标,得到结果.
(2)根据所给的直线的方程看出直线是一个过定点的直线,判断出定点在圆的内部,证明出直线与圆一定有交点,设PQ与l的夹角为θ,则d=|PQ|sinθ=
sinθ,得到当θ=90°时,d最大,|MN|最短,再写出直线的方程.
(2)根据所给的直线的方程看出直线是一个过定点的直线,判断出定点在圆的内部,证明出直线与圆一定有交点,设PQ与l的夹角为θ,则d=|PQ|sinθ=
| 5 |
解答:解:(1)由lAB:x-3y-6=0且AD⊥AB,点(-1,1)在边AD所在的直线上
∴AD所在直线的方程是:y-1=-3(x+1)即3x+y+2=0
由
得A(0,-2)…(3分)
∴|AP|=
=2
∴矩形ABCD的外接圆的方程是:(x-2)2+y2=8…(6分)
(2)直线l的方程可化为:k(-2x+y+4)+x+y-5=0l可看作是过直线-2x+y+4=0和x+y-5=0的交点(3,2)的直线系,即l恒过定点Q(3,2)
由于(3-2)2+22=5<8知点在圆内,
∴直线与圆恒有交点,
设PQ与l的夹角为θ,则d=|PQ|sinθ=
sinθ
当θ=90°时,d最大,|MN|最短,
此时l的斜率为PQ斜率的负倒数-
,
∴l:y-2=-
(x-3)
即x+2y-7=0
∴AD所在直线的方程是:y-1=-3(x+1)即3x+y+2=0
由
|
∴|AP|=
| 4+4 |
| 2 |
∴矩形ABCD的外接圆的方程是:(x-2)2+y2=8…(6分)
(2)直线l的方程可化为:k(-2x+y+4)+x+y-5=0l可看作是过直线-2x+y+4=0和x+y-5=0的交点(3,2)的直线系,即l恒过定点Q(3,2)
由于(3-2)2+22=5<8知点在圆内,
∴直线与圆恒有交点,
设PQ与l的夹角为θ,则d=|PQ|sinθ=
| 5 |
当θ=90°时,d最大,|MN|最短,
此时l的斜率为PQ斜率的负倒数-
| 1 |
| 2 |
∴l:y-2=-
| 1 |
| 2 |
即x+2y-7=0
点评:本题看出直线的方程和圆的方程的综合应用,本题解题的关键是写出圆的方程,再表示出圆的弦,求出最长的弦,本题是一个解析几何的综合题目.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
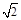 .将
.将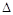 ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,
ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,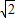 .将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )
.将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( ) .将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )
.将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )