题目内容
在正三棱柱
中，所有棱的长度都是2，
是
边的中点，问：在侧棱
上是否存在点
，使得异面直线
和
所成的角等于
．
在侧棱上不存在点，使得异面直线和所成的角等于
解析:
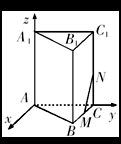
以
点为原点，建立如图所示的空间直角坐标系
．
因为所有棱长都等于2，所以
．
假设在侧棱
上存在点
，使得异面直线
与
所成的角等于
，
可设
，
则
．
于是，
．
因为异面直线和所成的角等于，
所以
和
的夹角是或
．
而
，
所以
，解得
，但由于
，
所以点不在侧棱上，
即在侧棱上不存在点，使得异面直线和所成的角等于．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
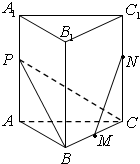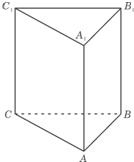
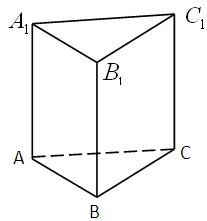
如图，在正三棱柱ABC-A1B1C1中，所有棱的长度都是1，M是BC边的中点，P是AA1边上的点，且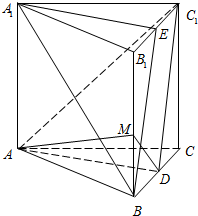
如图，在正三棱柱ABC-A1B1C1中，所有棱长都相等，点D，E分别是BC与B1C1的中点．