题目内容
为了打击“亚丁湾海盗”,确保我国来往索马里海域船只与船员的人身安全,中国派出了护航舰.一日,海面上A处的“武汉”号护航舰的雷达屏幕上发现在北偏西105°,相距40海里的B处有一海盗船,正按固定方向匀速直线航行,于是武汉号护航舰以 海里/小时的速度向正北方航行堵截,10分钟后航行到C处,发现海盗船位于北偏西方120°的D处,此时两船相距
海里/小时的速度向正北方航行堵截,10分钟后航行到C处,发现海盗船位于北偏西方120°的D处,此时两船相距 海里,问海盗船每小时行多少海里?
海里,问海盗船每小时行多少海里?
【答案】分析:由题意可以得出△ADC是等边三角形,计算出AC=AD=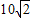 海里,再在△ABD中中利用余弦定理,求出BD的距离,根据所用的时间即可求出海盗船每小时行多少海里.
海里,再在△ABD中中利用余弦定理,求出BD的距离,根据所用的时间即可求出海盗船每小时行多少海里.
解答:解:如图所示,因为∠ACD=60°AC=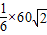 =
=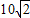 海里=DC,
海里=DC,
所以△ACD是等边三角形,AD═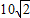 海里
海里
∵∠ABC=105°,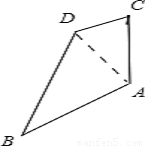
∴∠BAD=105°-60°=45°
在△ABD中,AB=40海里,AD═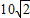 海里,
海里,
由余弦定理得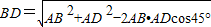 =10
=10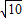 海里,
海里,
即B、D两处的距离等于A、B两处的距离是10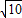 海里,
海里,
所以海盗船每小时行6BD=60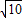 海里,
海里,
答:海盗船每小时行多少60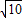 海里.
海里.
点评:本题主要考查了正余弦定理在解三角形中的应用,属于中档题.正确理解方向角的含义,合理选择三角形,是解决本题的关键.
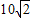 海里,再在△ABD中中利用余弦定理,求出BD的距离,根据所用的时间即可求出海盗船每小时行多少海里.
海里,再在△ABD中中利用余弦定理,求出BD的距离,根据所用的时间即可求出海盗船每小时行多少海里.解答:解:如图所示,因为∠ACD=60°AC=
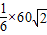 =
=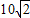 海里=DC,
海里=DC,所以△ACD是等边三角形,AD═
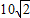 海里
海里∵∠ABC=105°,

∴∠BAD=105°-60°=45°
在△ABD中,AB=40海里,AD═
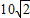 海里,
海里,由余弦定理得
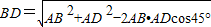 =10
=10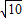 海里,
海里,即B、D两处的距离等于A、B两处的距离是10
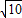 海里,
海里,所以海盗船每小时行6BD=60
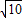 海里,
海里,答:海盗船每小时行多少60
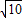 海里.
海里.点评:本题主要考查了正余弦定理在解三角形中的应用,属于中档题.正确理解方向角的含义,合理选择三角形,是解决本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目