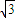题目内容
设双曲线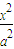 -
-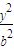 =1的一条渐进线l与圆
=1的一条渐进线l与圆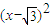 +y2=1只有一个公共点,则双曲线的离心率为( )
+y2=1只有一个公共点,则双曲线的离心率为( )A.

B.3
C.
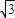
D.
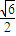
【答案】分析:先设出渐进线方程,把渐进线与圆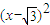 +y2=1只有一个公共点转化为圆心到直线的距离等于半径,即可求出之间的等量关系,再利用之间的关系即可求双曲线的离心率.
+y2=1只有一个公共点转化为圆心到直线的距离等于半径,即可求出之间的等量关系,再利用之间的关系即可求双曲线的离心率.
解答:解:设渐进线方程为y=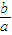 x⇒bx-ay=0,因为渐进线与圆
x⇒bx-ay=0,因为渐进线与圆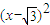 +y2=1只有一个公共点,所以有圆心到直线的距离等于半径,即1=
+y2=1只有一个公共点,所以有圆心到直线的距离等于半径,即1=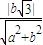 ⇒a2=2b2⇒a2=2(c2-a2)⇒c2=
⇒a2=2b2⇒a2=2(c2-a2)⇒c2= a2⇒e=
a2⇒e=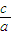 =
=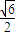 .
.
故选 D
点评:本题主要考查双曲线的几何性质,直线的方程以及点到直线的距离公式等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力.
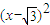 +y2=1只有一个公共点转化为圆心到直线的距离等于半径,即可求出之间的等量关系,再利用之间的关系即可求双曲线的离心率.
+y2=1只有一个公共点转化为圆心到直线的距离等于半径,即可求出之间的等量关系,再利用之间的关系即可求双曲线的离心率.解答:解:设渐进线方程为y=
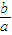 x⇒bx-ay=0,因为渐进线与圆
x⇒bx-ay=0,因为渐进线与圆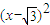 +y2=1只有一个公共点,所以有圆心到直线的距离等于半径,即1=
+y2=1只有一个公共点,所以有圆心到直线的距离等于半径,即1=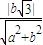 ⇒a2=2b2⇒a2=2(c2-a2)⇒c2=
⇒a2=2b2⇒a2=2(c2-a2)⇒c2= a2⇒e=
a2⇒e=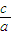 =
=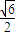 .
.故选 D
点评:本题主要考查双曲线的几何性质,直线的方程以及点到直线的距离公式等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力.

练习册系列答案
相关题目
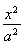
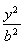
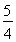
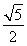
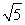
 -
- =1的一条渐进线l与圆
=1的一条渐进线l与圆 +y2=1只有一个公共点,则双曲线的离心率为( )
+y2=1只有一个公共点,则双曲线的离心率为( )