题目内容
正方形AP1P2P3的边长为4，点B，C分别是边P1P2，P2P3的中点，沿AB，BC，CA折成一个三棱锥P－ABC（使P1，P2，P3重合于P），则三棱锥P－ABC的外接球表面积为 （ ）
| A．24π | B．12π | C．8π | D．4π |
A
解析试题分析：沿AB，BC，CA折成一个三棱锥P－ABC，则三棱锥的三条侧棱两两垂直，故四面体P—ABC外接球的直径为以
为棱的球内接长方体的体对角线，由长方体的体对角线长
，
，故四面体P—ABC外接球的体积为
．
考点：球体的表面积公式，考查学生的空间想象能力.
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
一个正四棱锥和一个正四面体的所有棱长都相等，将它们的一个三角形重合在一起，组成一个新的几何体，则新几何体是（ ）
| A．五面体 | B．六面体 | C．七面体 | D．八面体 |
某几何体的三视图如图所示，则该几何体的体积是（ ）
A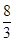． | B．4 | C．2 | D． |
如图，网格纸上小正方形的边长为1，粗线画的是某几何体的视图，则其体积为( )
A．12＋ | B．24＋ | C．32＋ | D．24＋ |
如图是一个几何体的三视图，则这个几何体的体积是 （ ）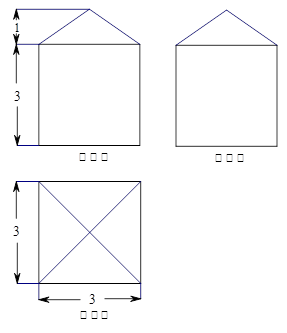
| A．27 | B．36 | C．33 | D．30 |
，在该几何体的正视图中，这条棱的投影是长为
的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，则a＋b的最大值为( )
，球面上有A、B、C三点，如果
，则三棱锥O-ABC 的体积为 （ ）
（B）
（C）1 （D）
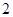的等边三角形,俯视图为圆,则该几何体的体积是( )
在透明塑料制成的正方体容器中灌进
体积的水，密封后可以任意摆放，那么容器内水面形状可能是：①三角形；②梯形；③长方形；④五边形．
其中正确的结果是 （ ）
| A．①②③ | B．①③④ | C．②③④ | D．①②③④ |