题目内容
三条直线相交于一点,可能确定的平面有( )
分析:根据平面的基本性质和空间直线的位置关系举例加以说明,可得当三条直线a、b、c相交于一点0时,它们可能确定α、β、γ三个平面,也可能确定一个平面.由此得到本题答案.
解答:解:①若平面α、β、γ两两相交,有三条交线,设三条交点分别为a、b、c,
则直线a、b、c交于一点O,此时三条直线确定3个平面;


②若直线a、b、c交于一点O,且直线a、b、c是平面α的相交直线,
此时直线a、b、c只能确定平面α,三条直线确定1个平面
综上所述,得三条直线相交于一点,可能确定的平面有1个或3个
故选:D
则直线a、b、c交于一点O,此时三条直线确定3个平面;


②若直线a、b、c交于一点O,且直线a、b、c是平面α的相交直线,
此时直线a、b、c只能确定平面α,三条直线确定1个平面
综上所述,得三条直线相交于一点,可能确定的平面有1个或3个
故选:D
点评:本题给出空间三条直线相交于一点,问它们能确定平面的个数.着重考查了空间直线的位置关系和平面的基本性质等知识,考查了空间想象能力,属于基础题.

练习册系列答案
相关题目
 如图,三条直线两两平行且不共面,每两条确定一个平面,一共可以确定几个平面?如果三条直线相交于一点,它们最多可以确定几个平面?
如图,三条直线两两平行且不共面,每两条确定一个平面,一共可以确定几个平面?如果三条直线相交于一点,它们最多可以确定几个平面?
 个 B.
个 B. 个 C.
个 C.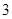 个 D.
个 D.