题目内容
设O为△ABC内一点,若任意k∈R,有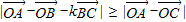 ,则△ABC的形状一定是( )
,则△ABC的形状一定是( )A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
【答案】分析:由题意可得|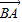 -k
-k 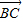 |≥|
|≥|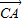 |,两边平方化简可得,关于k的不等式 a2•k2-2ac•cosB•k+c2-b2≥0恒成立,
|,两边平方化简可得,关于k的不等式 a2•k2-2ac•cosB•k+c2-b2≥0恒成立,
由判别式△≤0 化简可得 sin2B≥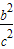 ,再由正弦定理求得 sin2C≥1,故有sinC=1,C=
,再由正弦定理求得 sin2C≥1,故有sinC=1,C=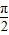 ,由此得出结论.
,由此得出结论.
解答:解:∵O为△ABC内一点,若任意k∈R,有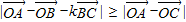 ,即|
,即|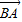 -k
-k 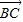 |≥|
|≥|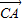 |.
|.
设△ABC的三边分别为a、b、c,把不等式|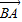 -k
-k 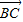 |≥|
|≥|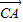 |两边平方可得:
|两边平方可得:
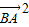 +k2
+k2 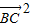 -2k
-2k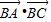 ≥
≥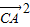 ,即 a2•k2-2ac•cosB•k+c2-b2≥0.
,即 a2•k2-2ac•cosB•k+c2-b2≥0.
由于k为任意实数,故关于k的不等式 a2•k2-2ac•cosB•k+c2-b2≥0恒成立.
故判别式△=4a2c2cos2B-4a2(c2-b2)≤0,化简可得 sin2B≥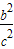 .
.
再由正弦定理可得 sin2B≥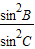 ,∴sin2C≥1.
,∴sin2C≥1.
由于C为△ABC的内角,故0<sinC≤1,故只有 sinC=1,∴C=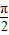 .
.
故△ABC的形状一定是直角三角形,
故选 B.
点评:本题主要考查函数的恒成立问题,正弦定理的应用,两个向量的数量积的运算,属于中档题.
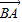 -k
-k 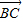 |≥|
|≥|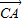 |,两边平方化简可得,关于k的不等式 a2•k2-2ac•cosB•k+c2-b2≥0恒成立,
|,两边平方化简可得,关于k的不等式 a2•k2-2ac•cosB•k+c2-b2≥0恒成立,由判别式△≤0 化简可得 sin2B≥
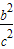 ,再由正弦定理求得 sin2C≥1,故有sinC=1,C=
,再由正弦定理求得 sin2C≥1,故有sinC=1,C=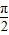 ,由此得出结论.
,由此得出结论.解答:解:∵O为△ABC内一点,若任意k∈R,有
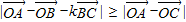 ,即|
,即|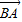 -k
-k 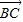 |≥|
|≥|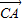 |.
|.设△ABC的三边分别为a、b、c,把不等式|
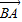 -k
-k 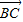 |≥|
|≥|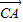 |两边平方可得:
|两边平方可得: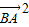 +k2
+k2 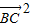 -2k
-2k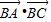 ≥
≥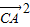 ,即 a2•k2-2ac•cosB•k+c2-b2≥0.
,即 a2•k2-2ac•cosB•k+c2-b2≥0.由于k为任意实数,故关于k的不等式 a2•k2-2ac•cosB•k+c2-b2≥0恒成立.
故判别式△=4a2c2cos2B-4a2(c2-b2)≤0,化简可得 sin2B≥
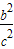 .
.再由正弦定理可得 sin2B≥
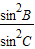 ,∴sin2C≥1.
,∴sin2C≥1.由于C为△ABC的内角,故0<sinC≤1,故只有 sinC=1,∴C=
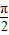 .
.故△ABC的形状一定是直角三角形,
故选 B.
点评:本题主要考查函数的恒成立问题,正弦定理的应用,两个向量的数量积的运算,属于中档题.

练习册系列答案
相关题目
设O为△ABC内一点,且满足
+
+
=
,则△AOB与△AOC的面积之比是( )
| 1 |
| 6 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 2 |
| OC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设O为△ABC内一点,若任意k∈R,有|
-
-k
| ≥ |
-
|,则△ABC的形状一定是( )
| OA |
| OB |
| BC |
| OA |
| OC |
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |
 (k > 0),
(k > 0), ,则k的值为_______________.
,则k的值为_______________. ,则△ABC的形状一定是( )
,则△ABC的形状一定是( )