题目内容
α∈(0,π),若
∈R,则α=( )
| sinα-cosα i |
| sinα+cosα i |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |
分析:利用复数的运算法则求得
=(sinα-cosα i)2展开后利用二倍角公式化简整理,利用原式为实数求得sin2α的值,进而求得α.
| sinα-cosα i |
| sinα+cosα i |
解答:解:
=(sinα-cosα i)2=-cos2α-sin2α i∈R
∴α=
故选B
| sinα-cosα i |
| sinα+cosα i |
∴α=
| π |
| 2 |
故选B
点评:本题主要考查了三角函数的化简求值,复数的基本运算.考查了学生知识的综合的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a,b,c为实数,f(x)=(x+a)(x2+bx+c),g(x)=(ax+1)(cx2+bx+1).记集合S={x|f(x)=0,x∈R},T={x|g(x)=0,x∈R}.若{S},{T}分别为集合S,T 的元素个数,则下列结论不可能的是( )
| A、{S}=1且{T}=0 | B、{S}=1且{T}=1 | C、{S}=2且{T}=2 | D、{S}=2且{T}=3 |
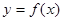 是增函数,且函数
是增函数,且函数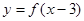 的图像关于(3,0)成中心对称,若s,t满足不等式
的图像关于(3,0)成中心对称,若s,t满足不等式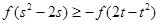 ,则
,则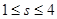 时,则
时,则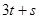 的范围是( )
的范围是( )