Question

过圆x²+y²-x+y-2=0和x²+y²=5的交点，且圆心在直线3x+4y-1=0上的圆的方程为     .

 

Answer 1

【答案】

(x+1)²+(y-1)²=13

【解析】

试题分析：设所求圆的方程为x²+y²-x+y-2+λ（x²+y²-5）=0（λ≠-1），

即整理可得,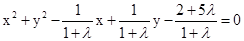

以可知圆心坐标为 (，-)，

因为圆心在直线3x+4y-1=0上，

所以可得3×-4×-1=0，

解得λ=-．将λ=-

代入所设方程并化简可得所求圆的方程为：x²+y²+2x-2y-11=0．

故答案为(x+1)²+(y-1)²=13．

考点：圆的方程

点评：中档题，确定圆的方程，常用方法是“待定系数法”。本题利用了“圆系方程”，通过确定一个待定系数，解决问题。