题目内容
【题目】在平面直角坐标系中,直线l的方程为x+y+3=0,以直角坐标系中x轴的正半轴为极轴的极坐标系中,圆M的极坐标方程为ρ=2sinθ. (Ⅰ)写出圆M的直角坐标方程及过点P(2,0)且平行于l的直线l1的参数方程;
(Ⅱ)设l1与圆M的两个交点为A,B,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)极坐标方程ρ=2sinθ两边同乘ρ,得ρ2=2ρsinθ 其中ρ2=x2+y2 , y=ρsinθ,x=ρcosθ
所以⊙M的直角坐标方程为x2+y2﹣2y=0…①
又直线x+y+3=0的倾斜角为 ![]() ,
,
所以过点P(2,0)且平行于x+y+3=0的直线的参数方程为 
即 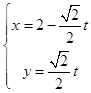 ,(t为参数)…②
,(t为参数)…②
直线的参数方程不唯一,只要正确给分
(Ⅱ)把(Ⅰ)中的②代入①整理得 ![]()
设方程的两根为t1 , t2 , 则有 ![]()
由参数t 的几何意义知PA+PB=t1+t2 , PA*PB=t1t2
所以 ![]()
【解析】(Ⅰ)极坐标方程ρ=2sinθ两边同乘ρ,得ρ2=2ρsinθ,从而能求出⊙M的直角坐标方程,直线x+y+3=0的倾斜角为 ![]() ,由此能求出过点P(2,0)且平行于x+y+3=0的直线的参数方程.(Ⅱ)把直线的参数方程代入圆的直角坐标方程,得
,由此能求出过点P(2,0)且平行于x+y+3=0的直线的参数方程.(Ⅱ)把直线的参数方程代入圆的直角坐标方程,得 ![]() ,由参数t 的几何意义能求出
,由参数t 的几何意义能求出 ![]() 的值.
的值.

练习册系列答案
相关题目

