题目内容
已知集合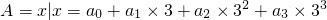 ,其中ak∈{0,1,2}(k=0,1,2,3),且a3≠0.则A中所有元素之和等于
,其中ak∈{0,1,2}(k=0,1,2,3),且a3≠0.则A中所有元素之和等于
- A.3240
- B.3120
- C.2997
- D.2889
D
分析:由题意可知a0,a1,a2各有3种取法(均可取0,1,2),a3有2种取法,利用数列求和即可求得A中所有元素之和.
解答:由题意可知,a0,a1,a2各有3种取法(均可取0,1,2),a3有2种取法,
由分步计数原理可得共有3×3×3×2种方法,
∴当a0取0,1,2时,a1,a2各有3种取法,a3有2种取法,共有3×3×2=18种方法,
即集合A中含有a0项的所有数的和为(0+1+2)×18;
同理可得集合A中含有a1项的所有数的和为(3×0+3×1+3×2)×18;
集合A中含有a2项的所有数的和为(32×0+32×1+32×2)×18;
集合A中含有a3项的所有数的和为(33×1+33×2)×27;
由分类计数原理得集合A中所有元素之和:
S=(0+1+2)×18+(3×0+3×1+3×2)×18+(32×0+32×1+32×2)×18+(33×1+33×2)×27
=18(3+9+27)+81×27
=702+2187
=2889.
故选D.
点评:本题考查数列的求和,考查分类计数原理与分步计数原理的应用,考查分类讨论与转化思想的综合应用,属于难题.
分析:由题意可知a0,a1,a2各有3种取法(均可取0,1,2),a3有2种取法,利用数列求和即可求得A中所有元素之和.
解答:由题意可知,a0,a1,a2各有3种取法(均可取0,1,2),a3有2种取法,
由分步计数原理可得共有3×3×3×2种方法,
∴当a0取0,1,2时,a1,a2各有3种取法,a3有2种取法,共有3×3×2=18种方法,
即集合A中含有a0项的所有数的和为(0+1+2)×18;
同理可得集合A中含有a1项的所有数的和为(3×0+3×1+3×2)×18;
集合A中含有a2项的所有数的和为(32×0+32×1+32×2)×18;
集合A中含有a3项的所有数的和为(33×1+33×2)×27;
由分类计数原理得集合A中所有元素之和:
S=(0+1+2)×18+(3×0+3×1+3×2)×18+(32×0+32×1+32×2)×18+(33×1+33×2)×27
=18(3+9+27)+81×27
=702+2187
=2889.
故选D.
点评:本题考查数列的求和,考查分类计数原理与分步计数原理的应用,考查分类讨论与转化思想的综合应用,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
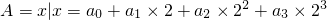 ,其中ak∈{0,1}(k=0,1,2,3),且a3≠0.则A中所有元素之和是
,其中ak∈{0,1}(k=0,1,2,3),且a3≠0.则A中所有元素之和是 ,其中ak∈{0,1}(k=0,1,2,3),且a3≠0.则A中所有元素之和是( )
,其中ak∈{0,1}(k=0,1,2,3),且a3≠0.则A中所有元素之和是( )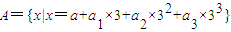 ,其中ak∈{0,1,2}(k=0,1,2,3),且a3≠0.则A中所有元素之和等于( )
,其中ak∈{0,1,2}(k=0,1,2,3),且a3≠0.则A中所有元素之和等于( )