题目内容
（2012•广东）已知函数
（其中ω＞0，x∈R）的最小正周期为10π．
（1）求ω的值；
（2）设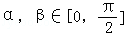
，
，
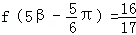，求cos（α+β）的值．
（1）
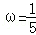（2）
解析
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
海淀课时新作业金榜卷系列答案期末金牌卷系列答案轻松课堂标准练系列答案题目内容
（2012•广东）已知函数（其中ω＞0，x∈R）的最小正周期为10π．
（1）求ω的值；
（2）设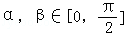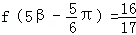，，，求cos（α+β）的值．
（1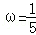） （2）
解析
海淀课时新作业金榜卷系列答案期末金牌卷系列答案轻松课堂标准练系列答案
cos（x+π）cosx，（x∈R）
=（
，
）平移后得到的函数y=g（x）的图象，求y=g（x）在（0，
、
的夹角为
（即
），现有可供建造第三面围墙的材料
米（两面墙的长均大于
，问当
为多少时，所建造的三角形露天仓库的面积最大，并求出最大值？ 
．
的终边过点
.
的值；
为第三象限角，且
，求
的值.
。（1）在一个周期内
如图所示，试根据图象写出
秒的时内I能同时取最大值|A|和最小值－|A|，那么正整数
的最小值为多少？
的图象过点
.
的值； 
的最小正周期及最大值.
, 设函数
. 
上的最大值和最小值.