题目内容
已知命题p:方程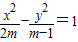 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线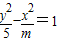 的离心率e∈(1,2),若p、q有且只有一个为真,求m的取值范围.
的离心率e∈(1,2),若p、q有且只有一个为真,求m的取值范围.
【答案】分析:根据题意求出命题p、q为真时m的范围分别为0<m< 、0<m<15.由p、q有且只有一个为真得p真q假,或p假q真,进而求出答案即可.
、0<m<15.由p、q有且只有一个为真得p真q假,或p假q真,进而求出答案即可.
解答:解:将方程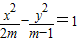 改写为
改写为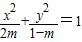 ,
,
只有当1-m>2m>0,即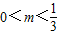 时,方程表示的曲线是焦点在y轴上的椭圆,所以命题p等价于
时,方程表示的曲线是焦点在y轴上的椭圆,所以命题p等价于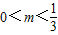 ;(4分)
;(4分)
因为双曲线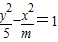 的离心率e∈(1,2),
的离心率e∈(1,2),
所以m>0,且1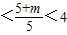 ,解得0<m<15,
,解得0<m<15,
所以命题q等价于0<m<15;…(8分)
若p真q假,则m∈∅;
若p假q真,则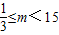
综上:m的取值范围为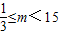 …(12分)
…(12分)
点评:本小题主要考查命题的真假判断与应用、椭圆的标准方程、双曲线的简单性质、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
 、0<m<15.由p、q有且只有一个为真得p真q假,或p假q真,进而求出答案即可.
、0<m<15.由p、q有且只有一个为真得p真q假,或p假q真,进而求出答案即可.解答:解:将方程
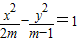 改写为
改写为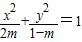 ,
,只有当1-m>2m>0,即
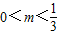 时,方程表示的曲线是焦点在y轴上的椭圆,所以命题p等价于
时,方程表示的曲线是焦点在y轴上的椭圆,所以命题p等价于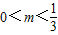 ;(4分)
;(4分)因为双曲线
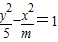 的离心率e∈(1,2),
的离心率e∈(1,2),所以m>0,且1
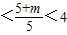 ,解得0<m<15,
,解得0<m<15,所以命题q等价于0<m<15;…(8分)
若p真q假,则m∈∅;
若p假q真,则
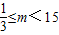
综上:m的取值范围为
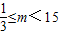 …(12分)
…(12分)点评:本小题主要考查命题的真假判断与应用、椭圆的标准方程、双曲线的简单性质、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
 是“方程
是“方程 ”表示椭圆的充要条件;
”表示椭圆的充要条件; 所表示的点在第二象限;
所表示的点在第二象限; 平面
平面 ,平面
,平面 ,则直线
,则直线 ,则下列复合命题中正确的是( )
,则下列复合命题中正确的是( )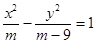 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线 的离心率
的离心率 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。 表示焦点在y轴上的椭圆;
表示焦点在y轴上的椭圆; 的离心率
的离心率 ,若p、q有且只有一个为真,求m的取值范围.
,若p、q有且只有一个为真,求m的取值范围. 表示焦点在y轴上的椭圆;
表示焦点在y轴上的椭圆; 的离心率
的离心率 ;
; ”为真,“
”为真,“ ”为假,求实数
”为假,求实数 的取值范围.
的取值范围. 表示双曲线,命题q:点(
表示双曲线,命题q:点( ,
, )在圆
)在圆 的内部. 若
的内部. 若 为假命题,
为假命题, 也为假命题,求实数
也为假命题,求实数 的取值范围
的取值范围