题目内容
已知函数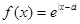 (
(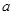 为常数). 若
为常数). 若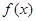 在区间
在区间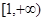 上是增函数,则
上是增函数,则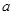 的取值范围是 .
的取值范围是 .
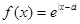 (
(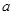 为常数). 若
为常数). 若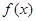 在区间
在区间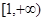 上是增函数,则
上是增函数,则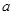 的取值范围是 .
的取值范围是 .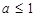
本试题主要是考查了指数型单调性的性质的运用。
因为函数f(x)=e|x-a|(a为常数).若f(x)在区间[1,+∞)上是增函数,由复合函数的单调性知,必有t=|x-a|在区间[1,+∞)上是增函数,又t=|x-a|在区间[a,+∞)上是增函数,所以[1,+∞)⊆[a,+∞),故有a≤1,故答案为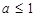 。
。
解决该试题的关键是作指数函数的图像,运用数形结合思想得到。
因为函数f(x)=e|x-a|(a为常数).若f(x)在区间[1,+∞)上是增函数,由复合函数的单调性知,必有t=|x-a|在区间[1,+∞)上是增函数,又t=|x-a|在区间[a,+∞)上是增函数,所以[1,+∞)⊆[a,+∞),故有a≤1,故答案为
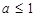 。
。解决该试题的关键是作指数函数的图像,运用数形结合思想得到。

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 =
= (ex-1)。
(ex-1)。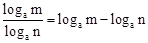
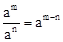
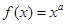 的图象经过点
的图象经过点 ,则
,则 .
. <b,且f (x)=
<b,且f (x)= ,则下列大小关系式成立的是 ( )
,则下列大小关系式成立的是 ( ) )<f (
)<f ( )
)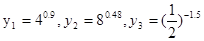 ,则( )
,则( )


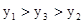
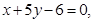 则
则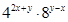 = .
= .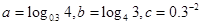 ,则( )
,则( )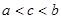
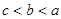


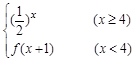 ,则
,则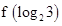 的值为 .
的值为 .