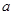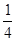题目内容
(本小题满分12分) 已知函数 (
( 且
且 )的图象过点
)的图象过点 ,点
,点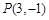 关于直线
关于直线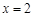 的对称点
的对称点 在
在 的图象上.
的图象上.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)令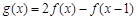 ,求
,求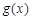 的最小值及取得最小值时x的值.
的最小值及取得最小值时x的值.
 (
( 且
且 )的图象过点
)的图象过点 ,点
,点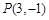 关于直线
关于直线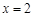 的对称点
的对称点 在
在 的图象上.
的图象上.(Ⅰ)求函数
 的解析式;
的解析式;(Ⅱ)令
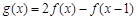 ,求
,求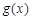 的最小值及取得最小值时x的值.
的最小值及取得最小值时x的值.(Ⅰ)函数解析式为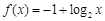 .(Ⅱ)当
.(Ⅱ)当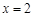 时,函数
时,函数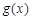 取得最小值1.
取得最小值1.
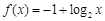 .(Ⅱ)当
.(Ⅱ)当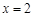 时,函数
时,函数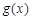 取得最小值1.
取得最小值1. 本试题主要是考查了哈数解析式的求解以及函数的最值问题的研究
(1)因为点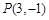 关于直线
关于直线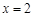 的对称点Q的坐标为
的对称点Q的坐标为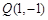 .再由由
.再由由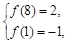 得
得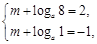 得到参数m,a的值,求得解析式。
得到参数m,a的值,求得解析式。
(2)因为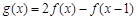
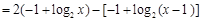
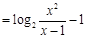 (
(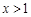 ),然后利用均值不等式得到最值。
),然后利用均值不等式得到最值。
(Ⅰ)点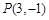 关于直线
关于直线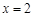 的对称点Q的坐标为
的对称点Q的坐标为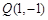 .·········· 2分
.·········· 2分
由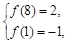 得
得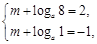 ······················· 4分
······················· 4分
解得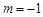 ,
,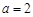 ,故函数解析式为
,故函数解析式为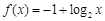 .············ 6分
.············ 6分
(Ⅱ)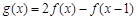
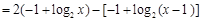
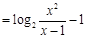 (
(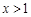 ),
),
····································· 8分
∵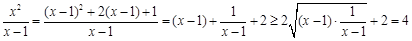 ,
,
当且仅当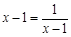 即
即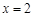 时,“=”成立, ················ 10分
时,“=”成立, ················ 10分
而函数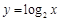 在
在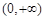 上单调递增,则
上单调递增,则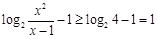 ,
,
故当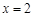 时,函数
时,函数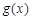 取得最小值1.··················· 12分
取得最小值1.··················· 12分
(1)因为点
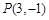 关于直线
关于直线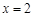 的对称点Q的坐标为
的对称点Q的坐标为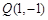 .再由由
.再由由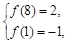 得
得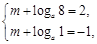 得到参数m,a的值,求得解析式。
得到参数m,a的值,求得解析式。(2)因为
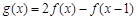
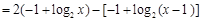
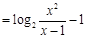 (
(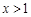 ),然后利用均值不等式得到最值。
),然后利用均值不等式得到最值。(Ⅰ)点
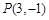 关于直线
关于直线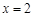 的对称点Q的坐标为
的对称点Q的坐标为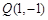 .·········· 2分
.·········· 2分由
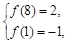 得
得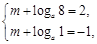 ······················· 4分
······················· 4分解得
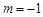 ,
,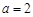 ,故函数解析式为
,故函数解析式为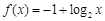 .············ 6分
.············ 6分(Ⅱ)
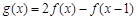
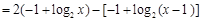
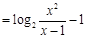 (
(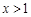 ),
),····································· 8分
∵
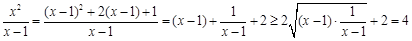 ,
,当且仅当
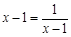 即
即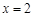 时,“=”成立, ················ 10分
时,“=”成立, ················ 10分而函数
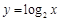 在
在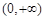 上单调递增,则
上单调递增,则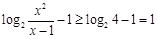 ,
,故当
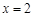 时,函数
时,函数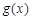 取得最小值1.··················· 12分
取得最小值1.··················· 12分
练习册系列答案
相关题目
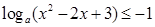 ,当
,当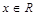 时恒成立.求
时恒成立.求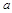 的取值范围.
的取值范围.
 的零点的个数为( )
的零点的个数为( ) ,且满足
,且满足
 的值;
的值; ,
, ,求
,求 的值。
的值。  ,若a <b,且f(a)=f(b),则a+2b的取值范围是________ .
,若a <b,且f(a)=f(b),则a+2b的取值范围是________ .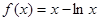 ,
,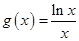 ,其中
,其中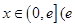 是自然常数).
是自然常数).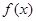 的单调性和极小值;
的单调性和极小值;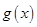 在
在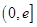 上单调递增;
上单调递增;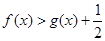 .
.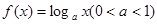 在区间
在区间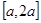 上的最大值是最小值的3倍,则
上的最大值是最小值的3倍,则