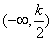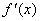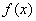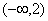题目内容

 设函数

   （I）k为何值时，f(x)在R上是减函数；

   （II）试确定实数k的值，使的极小值为0.

 

 

 

 

 

 

 

 

 

 

 

【答案】

 解：（Ⅰ）∵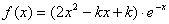

    ∴ 

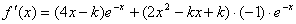
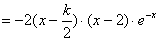
    当k=4时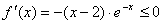，   ∴当k=4时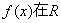，上是减函数

    （Ⅱ）当k≠4时，令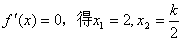

当k<4时，即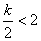有

x

（，2）

2

（2，+∞）

－

0

+

0

－

↘

极小

↗

极大

↘

令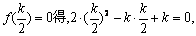  ∴k=0  ………………9分

②当k>4时，即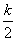>2有

x

2

（2，）

（，+∞）

－

0

+

0

－

↘

极小

↗

极大

↘

令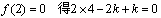   ∴k=8………………12分

∴当k=0或k=8时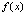，有极小值0   ………………13分

 

练习册系列答案
相关题目
在平行四边形OABC中，已知过点C的直线与线段OA，OB分别相交于点M，N．若
OM
=x
OA
，
ON
=y
OB
．
（1）求证：x与y的关系为y=
x
x+1
；
（2）设f(x)=
x
x+1
，定义函数F(x)=
1
f(x)
-1(0＜x≤1)，点列Pi（xi，F（xi））（i=1，2，…，n，n≥2）在函数F（x）的图象上，且数列{xn}是以首项为1，公比为
1
2
的等比数列，O为原点，令
OP
=
OP1
+
OP2
+…+
OPn
，是否存在点Q（1，m），使得
OP
⊥
OQ
？若存在，请求出Q点坐标；若不存在，请说明理由．
（3）设函数G（x）为R上偶函数，当x∈[0，1]时G（x）=f（x），又函数G（x）图象关于直线x=1对称，当方程G(x)=ax+
1
2
在x∈[2k，2k+2]（k∈N）上有两个不同的实数解时，求实数a的取值范围．

（13分）设函数

   （I）k为何值时，f(x)在R上是减函数；

   （II）试确定实数k的值，使的极小值为0.
在平行四边形OABC中，已知过点C的直线与线段OA，OB分别相交于点M，N．若
OM
=x
OA
，
ON
=y
OB
．
（1）求证：x与y的关系为y=
x
x+1
；
（2）设f(x)=
x
x+1
，定义函数F(x)=
1
f(x)
-1(0＜x≤1)，点列Pi（xi，F（xi））（i=1，2，…，n，n≥2）在函数F（x）的图象上，且数列{xn}是以首项为1，公比为
1
2
的等比数列，O为原点，令
OP
=
OP1
+
OP2
+…+
OPn
，是否存在点Q（1，m），使得
OP
⊥
OQ
？若存在，请求出Q点坐标；若不存在，请说明理由．
（3）设函数G（x）为R上偶函数，当x∈[0，1]时G（x）=f（x），又函数G（x）图象关于直线x=1对称，当方程G(x)=ax+
1
2
在x∈[2k，2k+2]（k∈N）上有两个不同的实数解时，求实数a的取值范围．

设函数f(x)=x+,A0为坐标原点,An为函数y=f(x)图象上横坐标为

n(n∈N*)的点,向量an=,向量i=(1,0),设θn为向量an与向量i的夹角,满足tanθk<的最大整数n是(　　)

A.2         B.3         C.4         D.5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网