题目内容
【题目】在四棱柱ABCD﹣A1B1C1D1中,AA1⊥底面ABCD,∠ADC=90°,AB∥CD,AD=CD=DD1=2AB=2. (Ⅰ) 求证:AD1⊥B1C;
(Ⅱ) 求二面角A1﹣BD﹣C1的正弦值.
【答案】证明:(Ⅰ)以D为坐标原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系D﹣xyz, 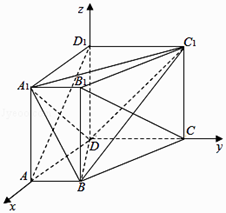
则A(2,0,0),A1(2,0,2),B(2,1,0),B1(2,1,2),C(0,2,0),C1(0,2,2),D1(0,0,2),
∴ ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,
,
∴AD1⊥B1C.
解:(Ⅱ) D(0,0,0), ![]() =(2,1,0),
=(2,1,0), ![]() =(2,0,2),
=(2,0,2), ![]() =(0,2,2),
=(0,2,2),
设平面A1BD的法向量为 ![]() ,
,
则由 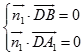 ,得
,得 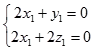 ,
,
取x1=1,得 ![]() ;
;
设平面C1BD的法向量为 ![]() ,
,
则由 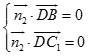 ,得
,得 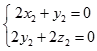 ,
,
取x2=1,得 ![]() ,
,
设二面角A1﹣BD﹣C1的平面角为θ,
则 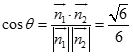 ,∴
,∴ ![]() .,
.,
∴二面角A1﹣BD﹣C1的正弦值为 ![]() .
.
【解析】(Ⅰ)以D为坐标原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系D﹣xyz,利用向量法能证明AD1⊥B1C.(2)求出平面A1BD的法向量和平面C1BD的法向量,由此利用向量法能求出二面角A1﹣BD﹣C1的正弦值.
【考点精析】通过灵活运用空间中直线与直线之间的位置关系,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点即可以解答此题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目