题目内容
设直线l1：y＝k1x＋1，l2：y＝k2x－1，其中实数k1，k2满足k1k2＋2＝0.
(1)证明l1与l2相交；
(2)证明l1与l2的交点在椭圆2x2＋y2＝1上．
[解答示范] 证明 (1)假设l1与l2不相交，
则l1与l2平行或重合，有k1＝k2，(2分)
代入k1k2＋2＝0，得k
＋2＝0.(4分)
这与k1为实数的事实相矛盾，从而k1≠k2，即l1与l2相交．(6分)
(2)由方程组
解得交点P的坐标(x，y)为
(9分)
从而2x2＋y2＝2
2＋
2
＝
＝
＝1，
此即表明交点P(x，y)在椭圆2x2＋y2＝1上．(12分)
练习册系列答案
相关题目
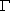的方程为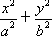
＝1(a＞b＞0)，A(0，b)、B(0，－b)和Q(a，0)为
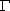的三个顶点．
，求点M的坐标；
于C、D两点，交直线l2∶y＝k2x于点E．若k1·k2＝
，证明：E为CD的中点；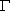
内且不在x轴上，如何构作过PQ中点F的直线l，使得l与椭圆
的两个交点P1，P2满足
？令a＝10，b＝5，点P的坐标是(－8，－1)．若椭圆
上的点P1，P2满足
，求点P1，P2的坐标．