题目内容
将函数f（x）=2sin（2x+
）-3的图形按向量
=（m，n）平移后得到函数g（x）的图形，满足g（
-x）=g（
+x）和g（-x）+g（x）=0，则向量
的一个可能值是（ ）
| π |
| 3 |
. |
| a |
| π |
| 4 |
| π |
| 4 |
. |
| a |
分析：由于函数g（x）的图形，满足g（
-x）=g（
+x）表示其图象关于直线x=
对称；满足g（-x）+g（x）=0，表示其是奇函数，图象关于原点对称，画出函数f（x）=2sin（2x+
）-3的图形，可知，其图形按向量
=（
，3）平移后得到函数g（x）的图形图象关于直线x=
对称，关于原点对称，从而得出正确选项．
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 3 |
. |
| a |
| π |
| 6 |
| π |
| 4 |
解答：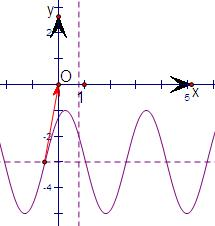
解：函数g（x）的图形，满足g（
-x）=g（
+x）表示其图象关于直线x=
对称；
满足g（-x）+g（x）=0，表示其是奇函数，图象关于原点对称，
画出函数f（x）=2sin（2x+
）-3的图形，可知，
其图形按向量
=（
，3）平移后得到函数g（x）的图形图象关于直线x=
对称，关于原点对称，
故选B．
解：函数g（x）的图形，满足g（| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
满足g（-x）+g（x）=0，表示其是奇函数，图象关于原点对称，
画出函数f（x）=2sin（2x+
| π |
| 3 |
其图形按向量
. |
| a |
| π |
| 6 |
| π |
| 4 |
故选B．
点评：本小题主要考查函数对称性的应用、函数奇偶性的应用、平面向量的综合题等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
将函数f（x）=2sin（2x-θ）-3的图象F按向量
=(
，3)，平移得到图象F′，若F′的一条对称轴是直线x=
，则θ的一个可能取值是（ ）
| a |
| π |
| 6 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|