题目内容
通过计算可得下列等式:
22-12=2×1+1;
32-22=2×2+1;
42-32=2×3+1;
…;
(n+1)2-n2=2n+1
将以上各式相加得:(n+1)2-12=2×(1+2+3+…+n)+n
所以可得:1+2+3+…+n=
.
类比上述求法:请你求出13+23+33+…+n3的值.(提示:12+22+32+…+n2=
)
22-12=2×1+1;
32-22=2×2+1;
42-32=2×3+1;
…;
(n+1)2-n2=2n+1
将以上各式相加得:(n+1)2-12=2×(1+2+3+…+n)+n
所以可得:1+2+3+…+n=
| n(n+1) |
| 2 |
类比上述求法:请你求出13+23+33+…+n3的值.(提示:12+22+32+…+n2=
| n(n+1)(2n+1) |
| 6 |
分析:类比12+22+…+n2的计算公式的推导过程,可得(n+1)4-n4=
×n3+
×n2+
×n+1,进而得叠加后可得4(13+23+…+n3),从而得到13+23+…+n3的计算公式.
| C | 1 4 |
| C | 2 4 |
| C | 3 4 |
解答:解:24-14=
×13+
×12+
×1+1,
34-24=
×23+
×22+
×2+1,
44-34=
×33+
×32+
×3+1,
…
(n+1)4-n4=
×n3+
×n2+
×n+1,
将以上各式相加得:(n+1)4-1=
(13+23+33+…+n3)+
(12+22+32+…+n2)+
(1+2+3+…+n)+n
=
(13+23+33+…+n3)+6•
+4•
+n,
∴13+23+33+…+n3=
•[(n+1)4-n(n+1)(2n+1)-2n(n+1)-(n+1)]
=
[(n+1)3-n(2n+1)-2n-1]=
[n3+3n2+3n+1-n(2n+1)-2n-1]=
[n3+n2]=[
]2.
| C | 1 4 |
| C | 2 4 |
| C | 3 4 |
34-24=
| C | 1 4 |
| C | 2 4 |
| C | 3 4 |
44-34=
| C | 1 4 |
| C | 2 4 |
| C | 3 4 |
…
(n+1)4-n4=
| C | 1 4 |
| C | 2 4 |
| C | 3 4 |
将以上各式相加得:(n+1)4-1=
| C | 1 4 |
| C | 2 4 |
| C | 3 4 |
=
| C | 1 4 |
| n(n+1)(2n+1) |
| 6 |
| n(n+1) |
| 2 |
∴13+23+33+…+n3=
| 1 |
| 4 |
=
| n+1 |
| 4 |
| n+1 |
| 4 |
| n+1 |
| 4 |
| n(n+1) |
| 2 |
点评:本题考查的知识点是类比推理,其中已知中的推理过程,类比得到(n+1)4-n4=
×n3+
×n2+
×n+1是解答的关键.
| C | 1 4 |
| C | 2 4 |
| C | 3 4 |

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
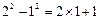 ,
,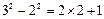 ,
,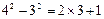 ,┅┅,
,┅┅,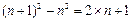
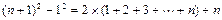
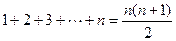
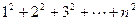 的值(要求必须有运算推理过程).
的值(要求必须有运算推理过程). ,
, ,
, ,┅┅,
,┅┅,


 的值(要求必须有运算推理过程).
的值(要求必须有运算推理过程).