题目内容
某厂家2008年拟举行促销活动,经调查测算,该产品的年销售量m万件(即该厂的年产量)与促销费用x万元(x≥0)满足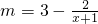 .已知2008年生产该产品m万件的成本C=16m+8万元,厂家将每件产品的销售价定为每件产品成本的1.5倍.
.已知2008年生产该产品m万件的成本C=16m+8万元,厂家将每件产品的销售价定为每件产品成本的1.5倍.
(Ⅰ)试将2008年该产品的利润y万元表示为年促销费用x万元的函数;
(Ⅱ)该厂家2008年的促销费用投入多少万元时,厂家的利润最大?
(利润=销售额-成本-促销费用)
解:(Ⅰ)依题意,得:利润函数y=(1.5-1)C-x=0.5(16m+8)-x
=8m+4-x=8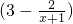 +4-x=28-
+4-x=28-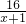 -x(其中x≥0);
-x(其中x≥0);
(Ⅱ)由(Ⅰ)得: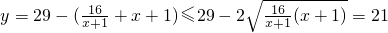
当且仅当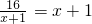 ,即x=3时取等号,
,即x=3时取等号,
所以,厂家2008年的促销费用投入3万元时,厂家的最大利润为21万元.
分析:(Ⅰ)根据“利润=销售额-成本-促销费用”得:利润函数y=(1.5-1)C-x,代入C,m整理即可;
(Ⅱ)由(Ⅰ)知,利润函数y的解析式,构造并应用基本不等式a+b≥2 (a>0,b>0),求出结果.
(a>0,b>0),求出结果.
点评:本题考查了利润函数模型的应用,同时考查了构造并应用基本不等式a+b≥2 (a>0,b>0),求函数最值问题,应用基本不等式时要注意等号成立的条件.
(a>0,b>0),求函数最值问题,应用基本不等式时要注意等号成立的条件.
=8m+4-x=8
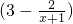 +4-x=28-
+4-x=28-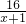 -x(其中x≥0);
-x(其中x≥0);(Ⅱ)由(Ⅰ)得:
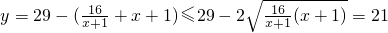
当且仅当
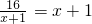 ,即x=3时取等号,
,即x=3时取等号,所以,厂家2008年的促销费用投入3万元时,厂家的最大利润为21万元.
分析:(Ⅰ)根据“利润=销售额-成本-促销费用”得:利润函数y=(1.5-1)C-x,代入C,m整理即可;
(Ⅱ)由(Ⅰ)知,利润函数y的解析式,构造并应用基本不等式a+b≥2
 (a>0,b>0),求出结果.
(a>0,b>0),求出结果.点评:本题考查了利润函数模型的应用,同时考查了构造并应用基本不等式a+b≥2
 (a>0,b>0),求函数最值问题,应用基本不等式时要注意等号成立的条件.
(a>0,b>0),求函数最值问题,应用基本不等式时要注意等号成立的条件. 
练习册系列答案
相关题目
 m3的油,则桶内剩余油量Q(m3)以流出时间t (分)为自变量的函数解析式是________.
m3的油,则桶内剩余油量Q(m3)以流出时间t (分)为自变量的函数解析式是________.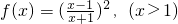 .
.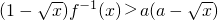 对一切
对一切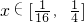 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.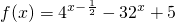 的最大值是________,最小值是________.
的最大值是________,最小值是________. ],若集合M={m|g(θ)<0},集合N={m|f[g(θ)]>0}.
],若集合M={m|g(θ)<0},集合N={m|f[g(θ)]>0}.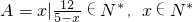 =________.
=________. ,这里我们称这一函数关系为“学习曲线”.已知这类学习任务中的某项任务有如下两组数据:t=4,y=50%;t=8,y=80%.
,这里我们称这一函数关系为“学习曲线”.已知这类学习任务中的某项任务有如下两组数据:t=4,y=50%;t=8,y=80%. ,问这项学习任务从哪一刻开始的2个单位时间内平均学习效率最高.
,问这项学习任务从哪一刻开始的2个单位时间内平均学习效率最高.