题目内容
已知
=(1,cosx),
=(sin2x,2cosx),且f(x)=
•
-1
(1)求函数y=f(x),x∈[0,π]的单调增区间;
(2)三角形ABC中,a,b,c分别为角A,B,C的对边,若b=
,c=1且f(A)=1,求a的值.
| a |
| b |
| a |
| b |
(1)求函数y=f(x),x∈[0,π]的单调增区间;
(2)三角形ABC中,a,b,c分别为角A,B,C的对边,若b=
| 2 |
分析:(1)易求f(x)=
sin(2x+
),当x∈[0,π]时,2x+
∈[
,
],利用正弦函数的单调性即可求得函数y=f(x)在x∈[0,π]的单调增区间;
(2)△ABC中,由f(A)=
sin(2A+
)=1,可求得A=
,利用余弦定理即可求得a的值.
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 9π |
| 4 |
(2)△ABC中,由f(A)=
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:解:(1)∵f(x)=
•
-1
=sin2x+1+cos2x-1
=
sin(2x+
),
∵x∈[0,π],
∴2x+
∈[
,
],
由
≤2x+
≤
与
≤2x+
≤
得0≤x≤
或
≤x≤π,
当x∈[0,π]时,f(x)的单调增区间为[0,
]和[
,π];
(2)∵f(A)=
sin(2A+
)=1,
∴sin(2A+
)=
,又三角形ABC中,A∈(0,π),
∴2A+
=
,解得A=
,
又b=
,c=1,
∴由余弦定理得:a2=b2+c2-2bccosA=2+1-2
×
=1,
∴a=1.
| a |
| b |
=sin2x+1+cos2x-1
=
| 2 |
| π |
| 4 |
∵x∈[0,π],
∴2x+
| π |
| 4 |
| π |
| 4 |
| 9π |
| 4 |
由
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| 9π |
| 4 |
| π |
| 8 |
| 5π |
| 8 |
当x∈[0,π]时,f(x)的单调增区间为[0,
| π |
| 8 |
| 5π |
| 8 |
(2)∵f(A)=
| 2 |
| π |
| 4 |
∴sin(2A+
| π |
| 4 |
| ||
| 2 |
∴2A+
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
又b=
| 2 |
∴由余弦定理得:a2=b2+c2-2bccosA=2+1-2
| 2 |
| ||
| 2 |
∴a=1.
点评:本题考查正弦函数的单调性,考查数量积的坐标于是与余弦定理,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤. 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E: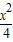
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E:
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E:
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.