题目内容
已知双曲线C的中心是原点,右焦点为F(
,0),焦点到一条渐近线距离为
,则双曲线C的渐近线方程为( )
| 3 |
| 2 |
A、y=±
| ||||
| B、y=±x | ||||
C、x=±
| ||||
D、x=±
|
分析:先根据双曲线的焦点坐标,求得a和b的关系,进而代入焦点到渐近线的距离,求得a和b,则双曲线的渐近线方程可得.
解答:解:依题意可知
,
解得a=1,b=
∴双曲线C的渐近线方程为y=±
x,即x=±
y
故选C
|
解得a=1,b=
| 2 |
∴双曲线C的渐近线方程为y=±
| 2 |
| ||
| 2 |
故选C
点评:本题主要考查了双曲线的简单性质,点到直线的距离.属基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
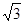 ,0),一条渐近线m:x+
,0),一条渐近线m:x+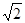 y=0,设过点A(-3
y=0,设过点A(-3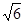 ,求k的值;
,求k的值;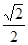 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为