题目内容
在锐角△ABC中,已知5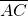 •
•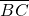 =4|
=4|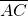 |•|
|•|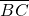 |,设
|,设 =(sinA,sinB),
=(sinA,sinB), =(cosB,-cosA)且
=(cosB,-cosA)且 •
• =
= ,
,
求:(1)sin(A+B)的值;(2)tanA的值.
解:(1)∵5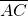 •
•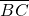 =5|
=5|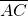 |•|
|•|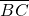 |cosC=4|
|cosC=4|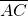 |•|
|•|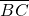 |,∴cosC=
|,∴cosC= ,…(2分)
,…(2分)
∴sin(A+B)=sinC= .
.
(2)设 x=tanA>0,∵ =sinAcosB-cosAsinB=
=sinAcosB-cosAsinB= ①,
①,
sin(A+B)=sinAcosB+cosAsinB= ②,
②,
由①+②可求得,sinAcosB= ,…(4分)
,…(4分)
∴cosAsinB= ,故tanAcotB=2,故 tanB=
,故tanAcotB=2,故 tanB= .
.
由(Ⅰ)可得cos(A+B)=- ,
,
故 tan(A+B)=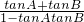 =
=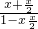 =
=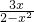 =-
=- ,
,
即 x2-4x-2=0,∴x=2+ ,∴tanA=2+
,∴tanA=2+ .
.
分析:(1)由条件利用两个向量的数量积的定义,求出cosC,再由诱导公式求出 sin(A+B)的值.
(2)设 x=tanA>0,由 =sinAcosB-cosAsinB=
=sinAcosB-cosAsinB= ,sin(A+B)=sinAcosB+cosAsinB=
,sin(A+B)=sinAcosB+cosAsinB= ,可得tanB=
,可得tanB= ,再由tan(A+B)=
,再由tan(A+B)=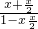 =-
=- ,解方程求出x的值,即为所求.
,解方程求出x的值,即为所求.
点评:本题主要考查两个向量的数量积的定义,两个向量数量积公式的应用,两角和的正切公式、正弦公式的应用,属于中档题
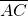 •
•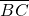 =5|
=5|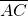 |•|
|•|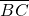 |cosC=4|
|cosC=4|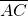 |•|
|•|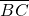 |,∴cosC=
|,∴cosC= ,…(2分)
,…(2分)∴sin(A+B)=sinC=
 .
. (2)设 x=tanA>0,∵
 =sinAcosB-cosAsinB=
=sinAcosB-cosAsinB= ①,
①,sin(A+B)=sinAcosB+cosAsinB=
 ②,
②,由①+②可求得,sinAcosB=
 ,…(4分)
,…(4分)∴cosAsinB=
 ,故tanAcotB=2,故 tanB=
,故tanAcotB=2,故 tanB= .
.由(Ⅰ)可得cos(A+B)=-
 ,
,故 tan(A+B)=
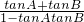 =
=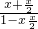 =
=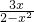 =-
=- ,
,即 x2-4x-2=0,∴x=2+
 ,∴tanA=2+
,∴tanA=2+ .
.分析:(1)由条件利用两个向量的数量积的定义,求出cosC,再由诱导公式求出 sin(A+B)的值.
(2)设 x=tanA>0,由
 =sinAcosB-cosAsinB=
=sinAcosB-cosAsinB= ,sin(A+B)=sinAcosB+cosAsinB=
,sin(A+B)=sinAcosB+cosAsinB= ,可得tanB=
,可得tanB= ,再由tan(A+B)=
,再由tan(A+B)=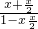 =-
=- ,解方程求出x的值,即为所求.
,解方程求出x的值,即为所求.点评:本题主要考查两个向量的数量积的定义,两个向量数量积公式的应用,两角和的正切公式、正弦公式的应用,属于中档题

练习册系列答案
相关题目