题目内容
已知扇形的周长为8,则其面积的最大值为 .
【答案】分析:设出半径和弧长,表示出周长和面积公式,根据基本不等式求出面积的最大值即可.
解答:解:设扇形半径为r,弧长为l,则周长为2r+l=8,面积为s= lr,
lr,
因为8=2r+l≥2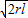 ,
,
所以r•l≤8,当且仅当l=2r时取等号.
因为s= lr,所以s≤4
lr,所以s≤4
故答案为:4
点评:本题考查扇形的周长和面积公式及利用基本不等式求最值,本题解题的关键是正确表示出扇形的面积,再利用基本不等式求解.
解答:解:设扇形半径为r,弧长为l,则周长为2r+l=8,面积为s=
 lr,
lr,因为8=2r+l≥2
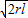 ,
,所以r•l≤8,当且仅当l=2r时取等号.
因为s=
 lr,所以s≤4
lr,所以s≤4故答案为:4
点评:本题考查扇形的周长和面积公式及利用基本不等式求最值,本题解题的关键是正确表示出扇形的面积,再利用基本不等式求解.

练习册系列答案
相关题目