题目内容
某竞猜活动有4人参加,设计者给每位参与者1道填空题和3道选择题,答对一道填空题得2分,答对一道选择题得1分,答错得0分,若得分总数大于或等于4分可获得纪念品,假定参与者答对每道填空题的概率为 ,答对每道选择题的概率为
,答对每道选择题的概率为 ,且每位参与者答题互不影响.
,且每位参与者答题互不影响.(Ⅰ)求某位参与竞猜活动者得3分的概率;
(Ⅱ)设参与者获得纪念品的人数为ξ,求随机变量ξ的分布列及数学期望.
【答案】分析:(Ⅰ)确定某位参与竞猜活动者得3分,包括答对一道填空题且只答对一道选择题、答错填空题且答对三道选择题,求出相应的概率,即可得到结论;
(Ⅱ)确定随机变量ξ的取值,求出相应的概率,可得分布列与期望.
解答:解:(Ⅰ)答对一道填空题且只答对一道选择题的概率为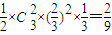 ,
,
答错填空题且答对三道选择题的概率为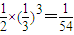 (对一个4分)
(对一个4分)
∴某位参与竞猜活动者得3分的概率为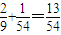 ; …(7分)
; …(7分)
(Ⅱ)由题意知随机变量ξ的取值有0,1,2,3,4.
又某位参与竞猜活动者得4分的概率为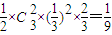
某位参与竞猜活动者得5分的概率为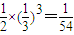
∴参与者获得纪念品的概率为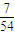 …(11分)
…(11分)
∴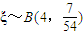 ,分布列为
,分布列为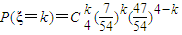 ,k=0,1,2,3,4
,k=0,1,2,3,4
即
∴随机变量ξ的数学期望Eξ=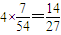 .…(14分)
.…(14分)
点评:本题考查概率的计算,考查离散型随机变量的分布列与期望,考查学生的计算能力,属于中档题.
(Ⅱ)确定随机变量ξ的取值,求出相应的概率,可得分布列与期望.
解答:解:(Ⅰ)答对一道填空题且只答对一道选择题的概率为
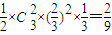 ,
,答错填空题且答对三道选择题的概率为
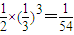 (对一个4分)
(对一个4分)∴某位参与竞猜活动者得3分的概率为
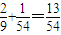 ; …(7分)
; …(7分)(Ⅱ)由题意知随机变量ξ的取值有0,1,2,3,4.
又某位参与竞猜活动者得4分的概率为
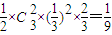
某位参与竞猜活动者得5分的概率为
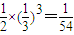
∴参与者获得纪念品的概率为
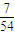 …(11分)
…(11分)∴
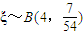 ,分布列为
,分布列为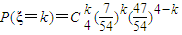 ,k=0,1,2,3,4
,k=0,1,2,3,4即
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | 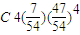 | 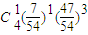 | 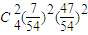 | 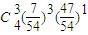 | 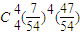 |
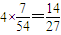 .…(14分)
.…(14分)点评:本题考查概率的计算,考查离散型随机变量的分布列与期望,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目