Question

(本小题满分12分)

已知数列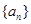是公差不为零的等差数列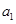，＝1，且成等比数列．

(1)求数列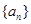的通项；

(2)设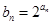，求数列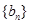的前n项和S_n.

 

Answer 1

【答案】

(1) a_n＝1＋(n－1)×1＝n. (2)S_n＝2^n＋1－2.

【解析】

试题分析：(1)由题设知公差d≠0，

由a₁＝1，a₁，a₃，a₉成等比数列得＝，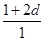

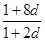解得d＝1，d＝0(舍去)，故{a_n}的通项a_n＝1＋(n－1)×1＝n. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分

(2)由(1)知2a_n＝2ⁿ，由等比数列前n项和公式得

S_n＝2＋2²＋2³＋…＋2ⁿ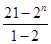＝＝2^n＋1－2. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分

考点：本题考查了数列的通项公式及前N项和

点评：掌握等差、等比数列的概念及前N项和公式是此类问题的关键。