题目内容
设数列{an}的前n项和为Sn,如果 为常数,则称数列{an}为“科比数列”.
为常数,则称数列{an}为“科比数列”.(Ⅰ)已知等差数列{bn}的首项为1,公差不为零,若{bn}为“科比数列”,求{bn}的通项公式;
(Ⅱ)设数列{cn}的各项都是正数,前n项和为Sn,若c13+c23+c33+…+cn3=Sn2对任意n∈N*都成立,试推断数列{cn}是否为“科比数列”?并说明理由.
【答案】分析:(Ⅰ)设等差数列{bn}的公差为d,根据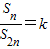 ,b1=1,整理得(4k-1)dn+(2k-1)(2-d)=0.因为对任意正整数n上式恒成立,进而可得关于k和d的方程组,求得k和d,进而求得{bn}的通项公式.
,b1=1,整理得(4k-1)dn+(2k-1)(2-d)=0.因为对任意正整数n上式恒成立,进而可得关于k和d的方程组,求得k和d,进而求得{bn}的通项公式.
(Ⅱ)先由题意求得a1,当n≥2时根据cn=Sn-Sn-1,求得数列{cn}的通项公式,进而代入 不是常数故推断数列{cn}不是“科比数列”.
不是常数故推断数列{cn}不是“科比数列”.
解答:解:(Ⅰ)设等差数列{bn}的公差为d(d≠0), ,因为b1=1,则
,因为b1=1,则 ,即2+(n-1)d=4k+2k(2n-1)d.
,即2+(n-1)d=4k+2k(2n-1)d.
整理得,(4k-1)dn+(2k-1)(2-d)=0.
因为对任意正整数n上式恒成立,则 ,解得
,解得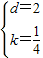 .
.
故数列{bn}的通项公式是bn=2n-1.
(Ⅱ)由已知,当n=1时,c13=S12=c12.因为c1>0,所以c1=1.
当n≥2时,c13+c23+c33++cn3=Sn2,c13+c23+c33++cn-13=Sn-12.
两式相减,得cn3=Sn2-Sn-12=(Sn-Sn-1)(Sn+Sn-1)=cn•(Sn+Sn-1).
因为cn>0,所以cn2=Sn+Sn-1=2Sn-cn.
显然c1=1适合上式,所以当n≥2时,cn-12=2Sn-1-cn-1.
于是cn2-cn-12=2(Sn-Sn-1)-cn+cn-1=2cn-cn+cn-1=cn+cn-1.
因为cn+cn-1>0,则cn-cn-1=1,所以数列{cn}是首项为1,公差为1的等差数列.
所以 不为常数,故数列{cn}不是“科比数列”.
不为常数,故数列{cn}不是“科比数列”.
点评:本题主要考查等差数列的通项公式和数列求和问题.考查了学生分析问题和解决问题的能力.
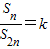 ,b1=1,整理得(4k-1)dn+(2k-1)(2-d)=0.因为对任意正整数n上式恒成立,进而可得关于k和d的方程组,求得k和d,进而求得{bn}的通项公式.
,b1=1,整理得(4k-1)dn+(2k-1)(2-d)=0.因为对任意正整数n上式恒成立,进而可得关于k和d的方程组,求得k和d,进而求得{bn}的通项公式.(Ⅱ)先由题意求得a1,当n≥2时根据cn=Sn-Sn-1,求得数列{cn}的通项公式,进而代入
 不是常数故推断数列{cn}不是“科比数列”.
不是常数故推断数列{cn}不是“科比数列”.解答:解:(Ⅰ)设等差数列{bn}的公差为d(d≠0),
 ,因为b1=1,则
,因为b1=1,则 ,即2+(n-1)d=4k+2k(2n-1)d.
,即2+(n-1)d=4k+2k(2n-1)d.整理得,(4k-1)dn+(2k-1)(2-d)=0.
因为对任意正整数n上式恒成立,则
 ,解得
,解得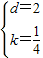 .
.故数列{bn}的通项公式是bn=2n-1.
(Ⅱ)由已知,当n=1时,c13=S12=c12.因为c1>0,所以c1=1.
当n≥2时,c13+c23+c33++cn3=Sn2,c13+c23+c33++cn-13=Sn-12.
两式相减,得cn3=Sn2-Sn-12=(Sn-Sn-1)(Sn+Sn-1)=cn•(Sn+Sn-1).
因为cn>0,所以cn2=Sn+Sn-1=2Sn-cn.
显然c1=1适合上式,所以当n≥2时,cn-12=2Sn-1-cn-1.
于是cn2-cn-12=2(Sn-Sn-1)-cn+cn-1=2cn-cn+cn-1=cn+cn-1.
因为cn+cn-1>0,则cn-cn-1=1,所以数列{cn}是首项为1,公差为1的等差数列.
所以
 不为常数,故数列{cn}不是“科比数列”.
不为常数,故数列{cn}不是“科比数列”.点评:本题主要考查等差数列的通项公式和数列求和问题.考查了学生分析问题和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目