题目内容
正方形ABCD的对角线AC在直线x+2y-1=0上,点A,B的坐标分别为A(-5,3),B(m,0)(m>-5),求B、C、D点的坐标.
分析:根据直线BD⊥AC,求出BD斜率为2,利用点斜式给出BD方程.将BD、AC方程联解可得E点关于m的坐标,由|AE|=|BE|列式解出m=-4,从而得到E点、B点的坐标,最后利用中点坐标公式可求出点C、D点的坐标,得到本题的答案.
解答: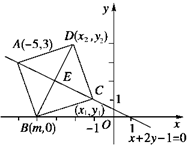 解:如图,设正方形ABCD两顶点C,D坐标分别为(x1,y1),(x2,y2).
解:如图,设正方形ABCD两顶点C,D坐标分别为(x1,y1),(x2,y2).
∵直线BD⊥AC,kAC=-
,∴kBD=
=2,
可得直线BD方程为y=2(x-m),
与x+2y-1=0联解,得
,
∴点E的坐标为(
+
m,
-
m),
又∵|AE|=|BE|,∴
=
,
平方整理,得m2+18m+56=0,解之得m=-4或m=-14(因为m>-5,舍去此解),
可得点B坐标为(-4,0),
∵点E坐标为(-3,2),E为AC中点
∴
,解之得
,即点C坐标为(-1,1),
同理可得点D坐标为(-2,4),
综上所述,点B(-4,0),点C(-1,1),点D(-2,4).
 解:如图,设正方形ABCD两顶点C,D坐标分别为(x1,y1),(x2,y2).
解:如图,设正方形ABCD两顶点C,D坐标分别为(x1,y1),(x2,y2).∵直线BD⊥AC,kAC=-
| 1 |
| 2 |
| -1 |
| kAC |
可得直线BD方程为y=2(x-m),
与x+2y-1=0联解,得
|
∴点E的坐标为(
| 1 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
又∵|AE|=|BE|,∴
(
|
(
|
平方整理,得m2+18m+56=0,解之得m=-4或m=-14(因为m>-5,舍去此解),
可得点B坐标为(-4,0),
∵点E坐标为(-3,2),E为AC中点
∴
|
|
同理可得点D坐标为(-2,4),
综上所述,点B(-4,0),点C(-1,1),点D(-2,4).
点评:本题给出正方形的对角线位置和一个顶点的坐标,求它另外顶点的坐标,着重考查了直线的基本形式、直线的位置关系和与直线关于直线对称的直线方程等知识,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
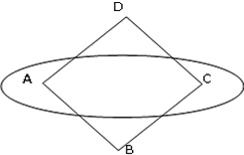 如图,椭圆以边长为1的正方形ABCD的对角顶点A,C为焦点,且经过各边的中点,试建立适当的坐标系,求椭圆的方程.
如图,椭圆以边长为1的正方形ABCD的对角顶点A,C为焦点,且经过各边的中点,试建立适当的坐标系,求椭圆的方程.