题目内容
已知两条直线l1:ax+by+c=0,直线l2:mx+ny+p=0,则an=bm是直线l1∥l2的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
B
分析:先由an=bm成立,看能否推出l1∥l2 成立,再由直线l1∥l2 成立,看能否推出an=bm 成立,然后依据充分条件、必要条件、充要条件的定义做出判断.
解答:①当an=bm时,若n、b都不等于0,则有 =
= ,-
,- =-
=- ,∴l1与l2的斜率相等,
,∴l1与l2的斜率相等,
但不知道它们在y轴上的截距- 和-
和- 是否相等,故两直线平行或重合,故不能推出l1∥l2,充分性不成立.
是否相等,故两直线平行或重合,故不能推出l1∥l2,充分性不成立.
②直线l1∥l2 时,若两直线的斜率都不存在,则n=b=0,an=bm成立.
若两直线的斜率都存在,则他们的斜率之积等于-1,即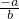 ×
×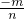 =-1,
=-1,
化简可得 an=bm,故一定能推出an=bm,必要性成立.
故选 B.
点评:本题考查充分条件、必要条件、充要条件的定义,分两个步骤进行判断,先看充分性是否成立,再看必要性是否成立,还要注意特殊情况(直线的斜率不存在),体现了分类讨论的数学思想.
分析:先由an=bm成立,看能否推出l1∥l2 成立,再由直线l1∥l2 成立,看能否推出an=bm 成立,然后依据充分条件、必要条件、充要条件的定义做出判断.
解答:①当an=bm时,若n、b都不等于0,则有
 =
= ,-
,- =-
=- ,∴l1与l2的斜率相等,
,∴l1与l2的斜率相等,但不知道它们在y轴上的截距-
 和-
和- 是否相等,故两直线平行或重合,故不能推出l1∥l2,充分性不成立.
是否相等,故两直线平行或重合,故不能推出l1∥l2,充分性不成立.②直线l1∥l2 时,若两直线的斜率都不存在,则n=b=0,an=bm成立.
若两直线的斜率都存在,则他们的斜率之积等于-1,即
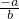 ×
×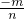 =-1,
=-1,化简可得 an=bm,故一定能推出an=bm,必要性成立.
故选 B.
点评:本题考查充分条件、必要条件、充要条件的定义,分两个步骤进行判断,先看充分性是否成立,再看必要性是否成立,还要注意特殊情况(直线的斜率不存在),体现了分类讨论的数学思想.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
已知两条直线l1:(m+3)x+4y+3m-5=0,l2:2x+(m+5)y-8=0,l1∥l2,则直线l1的一个方向向量是( )
A、(1,-
| ||
| B、(-1,-1) | ||
| C、(1,-1) | ||
D、(-1,-
|