题目内容
已知A、B、C是直线l上不同的三点,O是l外一点,向量 满足:
满足: 记y=f(x).
记y=f(x).
(1)求函数y=f(x)的解析式:
(2)若对任意 不等式
不等式 恒成立,求实数a的取值范围:
恒成立,求实数a的取值范围:
(3)若关于x的方程f(x)=2x+b在(0,1]上恰有两个不同的实根,求实数b的取值范围.
 满足:
满足: 记y=f(x).
记y=f(x).(1)求函数y=f(x)的解析式:
(2)若对任意
 不等式
不等式 恒成立,求实数a的取值范围:
恒成立,求实数a的取值范围:(3)若关于x的方程f(x)=2x+b在(0,1]上恰有两个不同的实根,求实数b的取值范围.
(1)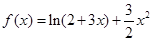 ;(2)
;(2)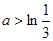 ;(3)
;(3)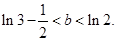 .
.
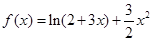 ;(2)
;(2)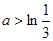 ;(3)
;(3)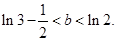 .
.试题分析:(1)根据条件中
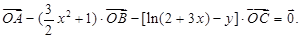 以及A,B,C三点共线可得
以及A,B,C三点共线可得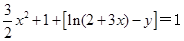 ,从而求得y的解析式;(2)要使
,从而求得y的解析式;(2)要使 在
在 上恒成立,只需
上恒成立,只需 ,通过求导判断
,通过求导判断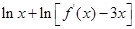 的单调性即可求得
的单调性即可求得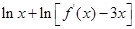 在
在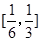 上的最大值,从而得到a的取值范围;(3)题中方程等价于
上的最大值,从而得到a的取值范围;(3)题中方程等价于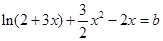 ,因此要使方程有两个不同的实根,只需求得
,因此要使方程有两个不同的实根,只需求得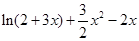 在(0,1]上的取值范围即可,通过求导判断单调性显然可以得到
在(0,1]上的取值范围即可,通过求导判断单调性显然可以得到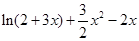 在(0,1]上的取值情况.
在(0,1]上的取值情况.(1)
 ,
,又∵A,B,C在同一直线上,∴
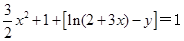 ,则
,则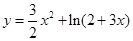 ,
,∴
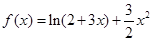 4分
4分(2)
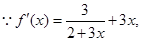 ∴
∴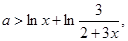 ① 5分
① 5分设
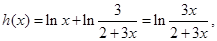 依题意知
依题意知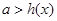 在
在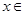
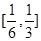 上恒成立,
上恒成立,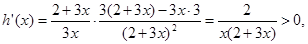 ∴h(x)在
∴h(x)在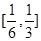 上是增函数,要使不等式①成立,当且仅当
上是增函数,要使不等式①成立,当且仅当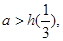 ∴
∴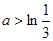 . 8分;
. 8分;(3)方程
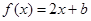 即为
即为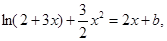 变形为
变形为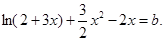
令
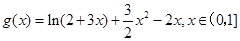 ,
,∴
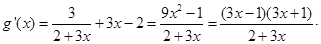 10分
10分列表写出 x,
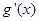 ,
,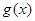 在[0,1]上的变化情况:
在[0,1]上的变化情况:| x | 0 | (0,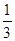 ) ) | 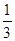 | (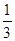 ,1) ,1) | 1 |
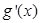 | | 小于0 | 取极小值 | 大于0 | |
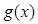 | ln2 | 单调递减 | 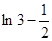 | 单调递增 | 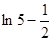 |
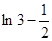 . 12分
. 12分现在比较ln2与
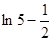 的大小;
的大小;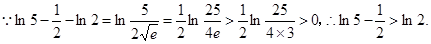
∴要使原方程在(0,1]上恰有两个不同的实根,必须使
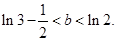
即实数b的取值范围为
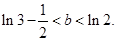 14分.
14分.
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
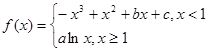
 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点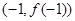 处的切线的斜率是
处的切线的斜率是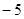 .
.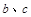 的值;
的值;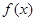 在区间
在区间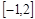 上的最大值;
上的最大值;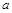 ,曲线
,曲线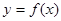 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得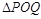 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在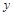 轴上?说明理由.
轴上?说明理由. ,其中e为自然对数的底数.
,其中e为自然对数的底数. 是增函数,求实数
是增函数,求实数 的取值范围;
的取值范围; 时,求函数
时,求函数 上的最小值;
上的最小值; .
.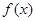 是定义在
是定义在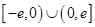 上的奇函数,当
上的奇函数,当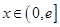 时,
时, 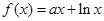 (其中e是自然界对数的底,
(其中e是自然界对数的底,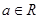 )
)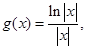 ,求证:当
,求证:当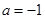 时,且
时,且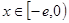 ,
, 恒成立;
恒成立;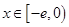 时,
时,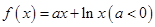 .
.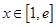 时,函数
时,函数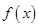 的最大值为
的最大值为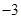 ,求
,求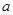 的值;
的值;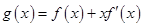 (
(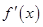 为函数
为函数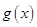 在
在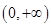 上是单调函数,求
上是单调函数,求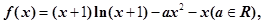
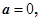 求函数
求函数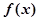 的极值点及相应的极值;
的极值点及相应的极值;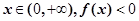 恒成立,求实数
恒成立,求实数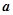 的取值范围.
的取值范围.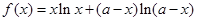
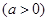 .
.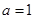 时,求函数
时,求函数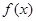 的最小值;
的最小值; ,都有
,都有 ;
;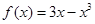 的单调减区间是
的单调减区间是