题目内容
在如图所示的多面体中，
，
．
（Ⅰ）求证：
；
（Ⅱ）求证：
．
证明过程详见试题解析.
【解析】
试题分析：（Ⅰ）由线线垂直得到线面垂直，再根据直线所在的平面得到线线垂直；（Ⅱ）根据性质定理：“一条直线与一个平面平行，那么过这条直线作一个平面与此平面相交，那么该直线与交线平行.”来证明.
试题解析：（Ⅰ）证明：因为
，
， 又
，
平面
,所以
平面.由于
平面， 所以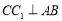
.
（Ⅱ）证明：因为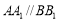
，又
平面
，
平面，所以
平面， 而
平面
，平面
平面
，所以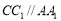
．
考点：（Ⅰ）线面垂直的性质定理；（Ⅱ）线面平行的性质定理.
练习册系列答案
相关题目
