题目内容
【题目】如图所示,四棱锥P﹣ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB= ![]() CD=1,M为PB的中点.
CD=1,M为PB的中点. 
(1)试在CD上确定一点N,使得MN∥平面PAD;
(2)点N在满足(1)的条件下,求直线MN与平面PAB所成角的正弦值.
【答案】
(1)证明:CN= ![]() ND,MN∥平面PAD.
ND,MN∥平面PAD.
过M作ME∥AB交PA于E,连接DE.
∵CN= ![]() ND,
ND,
∴CN= ![]() CD=
CD= ![]() AB=EM.
AB=EM.
又EM∥DC∥AB,∴EM∥DN,且EM=DN
∴DEMN为平行四边形,
∴MN∥DE,
又DE平面PAD,MN平面PAD,
∴MN∥平面PAD
(2)解:∵MN∥DE
∴直线MN与平面PAB所成角等于直线DE与平面PAB所成角
∵PA⊥底面ABCD,
∴PA⊥AD,
∵AB⊥AD,PA∩AB=A,
∴AD⊥平面PAB,
∴∠AED为直线DE与平面PAB所成角.
∵AE= ![]() ,AD=1,
,AD=1,
∴DE= ![]() ,
,
∴sin∠AED= ![]() =
= ![]() .
.
∴直线MN与平面PAB所成角的正弦值为 ![]()
【解析】(1)CN= ![]() ND,MN∥平面PAD,过M作ME∥AB交PA于E,连接DE,证明MN∥DE即可;(2)利用MN∥DE,考的直线MN与平面PAB所成角等于直线DE与平面PAB所成角.解△AED即可.
ND,MN∥平面PAD,过M作ME∥AB交PA于E,连接DE,证明MN∥DE即可;(2)利用MN∥DE,考的直线MN与平面PAB所成角等于直线DE与平面PAB所成角.解△AED即可.
【考点精析】本题主要考查了直线与平面平行的判定和空间角的异面直线所成的角的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则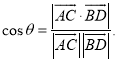 才能正确解答此题.
才能正确解答此题.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案【题目】某校夏令营有3名男同学A、B、C和3名女同学X,Y,Z,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
(1)用表中字母列举出所有可能的结果;
(2)设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.