题目内容
已知函数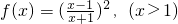 .
.
(1)求f(x)的反函数f-1(x);
(2)若不等式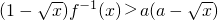 对一切
对一切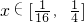 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
解:(1)由 得
得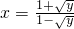 ,x>1,
,x>1,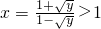 ,
,
∴0<y<1
∴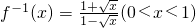
(2)由题设有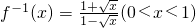 .
.
∴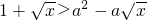 ,即
,即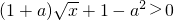 对任意的
对任意的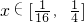 恒成立,显然a≠-1,
恒成立,显然a≠-1,
令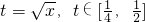 则g(t)=(1+a)t+1-a2>0对任意
则g(t)=(1+a)t+1-a2>0对任意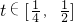 恒成立.
恒成立.
∴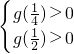 即
即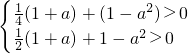 ,解得
,解得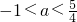 .
.
分析:(1)欲求原函数f(x)的反函数,即从原函数式中反解出x,后再进行x,y互换,即得反函数的解析式,再根据原函数的值域为反函数的定义域;
(2)将解析式代入化简,令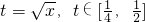 ,转化成关于t的一次不等式在
,转化成关于t的一次不等式在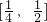 上恒成立,建立不等式组,解之即可.
上恒成立,建立不等式组,解之即可.
点评:本题主要考查了反函数,以及函数恒成立问题,同时考查了计算能力和转化的思想,属于基础题.
 得
得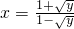 ,x>1,
,x>1,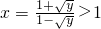 ,
,∴0<y<1
∴
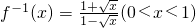
(2)由题设有
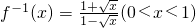 .
.∴
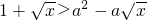 ,即
,即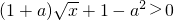 对任意的
对任意的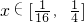 恒成立,显然a≠-1,
恒成立,显然a≠-1,令
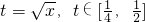 则g(t)=(1+a)t+1-a2>0对任意
则g(t)=(1+a)t+1-a2>0对任意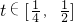 恒成立.
恒成立.∴
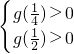 即
即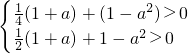 ,解得
,解得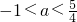 .
.分析:(1)欲求原函数f(x)的反函数,即从原函数式中反解出x,后再进行x,y互换,即得反函数的解析式,再根据原函数的值域为反函数的定义域;
(2)将解析式代入化简,令
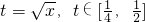 ,转化成关于t的一次不等式在
,转化成关于t的一次不等式在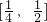 上恒成立,建立不等式组,解之即可.
上恒成立,建立不等式组,解之即可.点评:本题主要考查了反函数,以及函数恒成立问题,同时考查了计算能力和转化的思想,属于基础题.

练习册系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.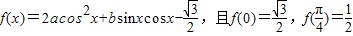 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.