Question

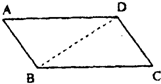如图所示，在平行四边形ABCD中，

AB

•

BD

=0，且2

AB2

+

BD2

=1，沿BD折在直二面角A-BD-C，则三棱锥A-BCD的外接球的体积是（　　）

• A、

  π

  27

• B、

  π

  12

• C、

  π

  8

• D、

  π

  6

Answer 1

分析：由已知中在平行四边形ABCD中，

AB

•

BD

=0，且2

AB2

+

BD2

=1，沿BD折在直二面角A-BD-C，则三棱锥A-BCD的外接球即为以AB，BD，DC为同一顶点三条棱的长方体的外接球，由此计算出外接球的半径，代入球的体积公式，即可得到答案．

解答：解：∵平行四边形ABCD中，

AB

•

BD

=0，且2

AB2

+

BD2

=1，
即AB⊥BD，BD⊥AC，AB²+BD²+DC²=1
则三棱锥A-BCD的外接球的直径2R=1
则R=

1

2

则V=

4

3

πR3=

π

6

故选D

点评：本题考查的知识点是球内接多面体，平面向量数量积的表示线段垂直，球的体积公式，其中根据已知条件计算出三棱锥A-BCD的外接球的半径是解答本题的关键．