题目内容
已知动圆过定点F(0,2),且与定直线L:y=-2相切。
(1)求动圆圆心的轨迹C的方程;
(2)若AB是轨迹C的动弦,且AB过F(0,2),分别以A、B为切点作轨迹C的切线,设两切线交点为Q,证明:AQ⊥BQ。
(1)求动圆圆心的轨迹C的方程;
(2)若AB是轨迹C的动弦,且AB过F(0,2),分别以A、B为切点作轨迹C的切线,设两切线交点为Q,证明:AQ⊥BQ。
(1)解:依题意,圆心的轨迹是以F(0,2)为焦点,L:y=-2为准线的抛物线上,
因为抛物线焦点到准线距离等于4,
所以圆心的轨迹是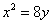 。
。
(2)证明:∵直线AB与x轴不垂直,设AB:y=kx+2,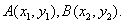 ,
,
由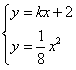 ,可得
,可得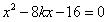 ,
,
∴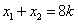 ,
,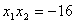 ,
,
抛物线的方程为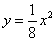 ,求导得
,求导得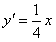 ,
,
所以过抛物线上A、B两点的切线斜率分别是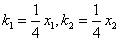 ,
,
∴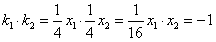
所以,AQ⊥BQ。
因为抛物线焦点到准线距离等于4,
所以圆心的轨迹是
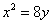 。
。(2)证明:∵直线AB与x轴不垂直,设AB:y=kx+2,
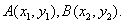 ,
,由
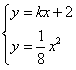 ,可得
,可得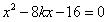 ,
,∴
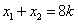 ,
,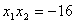 ,
,抛物线的方程为
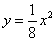 ,求导得
,求导得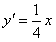 ,
,所以过抛物线上A、B两点的切线斜率分别是
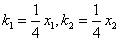 ,
,∴
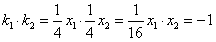
所以,AQ⊥BQ。

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目