题目内容
我们把各位数字之和为7的四位数称为“北斗数”(如2014是“北斗数”).则“北斗数”中千位为2的共有 个.
21
由题意,“北斗数”的后三位数字之和为5,三个数字只有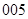 ,
, ,
,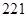 ,
,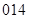 ,
,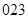 这五种可能,所以所求“北斗数“的个数为
这五种可能,所以所求“北斗数“的个数为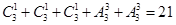 .
.
【考点】新定义概念与排列组合.
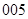 ,
, ,
,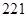 ,
,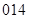 ,
,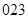 这五种可能,所以所求“北斗数“的个数为
这五种可能,所以所求“北斗数“的个数为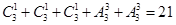 .
.【考点】新定义概念与排列组合.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
题目内容
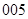 ,
, ,
,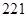 ,
,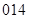 ,
,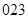 这五种可能,所以所求“北斗数“的个数为
这五种可能,所以所求“北斗数“的个数为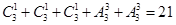 .
.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案