题目内容
已知x,y满足
.
(1)求z=x-2y的最大值和最小值;
(2)求μ=x2+y2-4x-8y+20的最小值.
|
(1)求z=x-2y的最大值和最小值;
(2)求μ=x2+y2-4x-8y+20的最小值.
分析:作出不等式组表示的可行域
(1)目标函数z=x-2y变为y=
x-
,截距为-
,结合图形可求z的最小值和最大值
(2)μ=x2+y2-4x-8y+20变为μ=(x-2)2+(y-4)2,μ表示点P(x,y)与点Q(2,4)两点间距离的平方,结合图形可求
(1)目标函数z=x-2y变为y=
| 1 |
| 2 |
| z |
| 2 |
| z |
| 2 |
(2)μ=x2+y2-4x-8y+20变为μ=(x-2)2+(y-4)2,μ表示点P(x,y)与点Q(2,4)两点间距离的平方,结合图形可求
解答: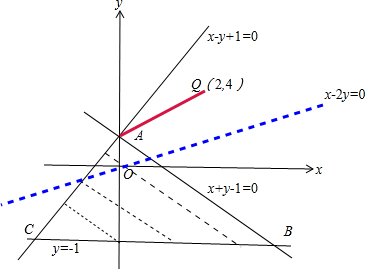 解:作出不等式组
解:作出不等式组
表示的可行域如图所示:
(1)目标函数z=x-2y变为y=
x-
,
它表示斜率为
,截距为-
的直线,
当直线y=
x平行移动到点A时,截距-
最小,
此时B(2,-1),zmax=4;
当直线y=
x平行移动到点B时,截距-
最大,此时A(0,1),zmin=-2;
(2)μ=x2+y2-4x-8y+20变为μ=(x-2)2+(y-4)2,μ表示点P(x,y)与点Q(2,4)两点间距离的平方,
由图可知,μmin=13
 解:作出不等式组
解:作出不等式组
|
(1)目标函数z=x-2y变为y=
| 1 |
| 2 |
| z |
| 2 |
它表示斜率为
| 1 |
| 2 |
| z |
| 2 |
当直线y=
| 1 |
| 2 |
| z |
| 2 |
此时B(2,-1),zmax=4;
当直线y=
| 1 |
| 2 |
| z |
| 2 |
(2)μ=x2+y2-4x-8y+20变为μ=(x-2)2+(y-4)2,μ表示点P(x,y)与点Q(2,4)两点间距离的平方,
由图可知,μmin=13
点评:本题主要考查了利用线性目标函数的几何意义及两点间的距离公式的简单应用,体现了数形结合思想的应用

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目