题目内容
 如图,把长、宽分别为4、3的长方形ABCD沿对角线AC折成直二面角.
如图,把长、宽分别为4、3的长方形ABCD沿对角线AC折成直二面角.(Ⅰ)求顶点B和D之间的距离;
(Ⅱ)现发现BC边上距点C的
| 1 | 3 |
分析:(Ⅰ)在△ABC中,过B作BO⊥AC,垂足为O,连接OD,利用面面垂直,可得BO⊥OD,进而利用Rt△BOD中,BO=
,OD=
,可求BD=
.
(Ⅱ)两种方案:方案(一)过E作EF∥AC交AB于F,EG∥CD,交BD于G,可知平面EFG∥平面ACD,从而可求原三棱锥被分成三棱锥B-EFG和三棱台EFG-CAD两部分体积比;方案(二)过E作EP∥BD交CD于P,EQ∥AB,交AC于Q,同(一)可证平面EPQ∥平面ABD,原三棱锥被分割成三棱锥C-EPQ和三棱台EPQ-BDA两部分体积比,从而可确定方案.
| 12 |
| 5 |
| ||
| 5 |
| ||
| 5 |
(Ⅱ)两种方案:方案(一)过E作EF∥AC交AB于F,EG∥CD,交BD于G,可知平面EFG∥平面ACD,从而可求原三棱锥被分成三棱锥B-EFG和三棱台EFG-CAD两部分体积比;方案(二)过E作EP∥BD交CD于P,EQ∥AB,交AC于Q,同(一)可证平面EPQ∥平面ABD,原三棱锥被分割成三棱锥C-EPQ和三棱台EPQ-BDA两部分体积比,从而可确定方案.
解答: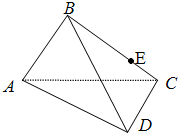 解:(Ⅰ)在△ABC中,过B作BO⊥AC,垂足为O,连接OD
解:(Ⅰ)在△ABC中,过B作BO⊥AC,垂足为O,连接OD
⇒
∴BO⊥OD
由已知BO=
,OD=
在Rt△BOD中,BD=
.
(Ⅱ)方案(一)过E作EF∥AC交AB于F,EG∥CD,交BD于G,
EF∩EG=E
∴平面EFG∥平面ACD
原三棱锥被分成三棱锥B-EFG和三棱台EFG-CAD两部分,此时
=(
)3=
.
方案(二)过E作EP∥BD交CD于P,EQ∥AB,交AC于Q,同(一)可证平面EPQ∥平面ABD,原三棱锥被分割成三棱锥C-EPQ和三棱台EPQ-BDA两部分,此时
=(
)3=
,
为使截去部分体积最小,
故选用方案(二).
 解:(Ⅰ)在△ABC中,过B作BO⊥AC,垂足为O,连接OD
解:(Ⅰ)在△ABC中,过B作BO⊥AC,垂足为O,连接OD
|
|
∴BO⊥OD
由已知BO=
| 12 |
| 5 |
| ||
| 5 |
| ||
| 5 |
(Ⅱ)方案(一)过E作EF∥AC交AB于F,EG∥CD,交BD于G,
|
|
∴平面EFG∥平面ACD
原三棱锥被分成三棱锥B-EFG和三棱台EFG-CAD两部分,此时
| VB-EFG |
| VB-ACD |
| 2 |
| 3 |
| 8 |
| 27 |
方案(二)过E作EP∥BD交CD于P,EQ∥AB,交AC于Q,同(一)可证平面EPQ∥平面ABD,原三棱锥被分割成三棱锥C-EPQ和三棱台EPQ-BDA两部分,此时
| VC-EPQ |
| VC-BDA |
| 1 |
| 3 |
| 1 |
| 27 |
为使截去部分体积最小,
故选用方案(二).
点评:本题以平面图形的翻折为载体,考查面面垂直的性质,考查几何体的体积,考查学生分析解决问题的能力.

练习册系列答案
相关题目
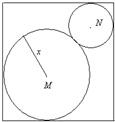 如图,在矩形ABCD内,两个圆M、N分别与矩形两边相切,且两圆互相外切.若矩形的长和宽分别为9和8,试把两个圆的面积之和S表示为圆M半径x的函数关系式,并求S的最大值和最小值.
如图,在矩形ABCD内,两个圆M、N分别与矩形两边相切,且两圆互相外切.若矩形的长和宽分别为9和8,试把两个圆的面积之和S表示为圆M半径x的函数关系式,并求S的最大值和最小值.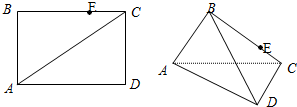
 处有一缺口E,请过点E作一截面,将原三棱锥分割成一个三棱锥和一个棱台两部分,为使截去部分体积最小,如何作法?请证明你的结论.
处有一缺口E,请过点E作一截面,将原三棱锥分割成一个三棱锥和一个棱台两部分,为使截去部分体积最小,如何作法?请证明你的结论.
 处有一缺口E,请过点E作一截面,将原三棱锥分割成一个三棱锥和一个棱台两部分,为使截去部分体积最小,如何作法?请证明你的结论.
处有一缺口E,请过点E作一截面,将原三棱锥分割成一个三棱锥和一个棱台两部分,为使截去部分体积最小,如何作法?请证明你的结论.