题目内容
（本小题满分12分）（注意：在试题卷上作答无效）
设定义在R上的函数
，当时，f (x)取得极大值，并且函数
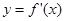的图象关于y轴对称。
（Ⅰ）求f (x)的表达式；
（Ⅱ）若曲线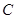
对应的解析式为
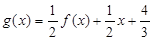，求曲线过点
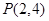的切线方程。
【答案】
（Ⅰ）f¢ (x)＝2x2－1
（Ⅱ）切线方程为：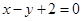
和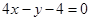
【解析】解：（1）∵
为偶函数，∴ f ¢(-x) = f ¢(x),
∴ 3ax2 -2bx + c= 3ax2 +2bx + c,
∴ 2bx =0对一切x Î R恒成立，∴ b＝0，………………………………2分
∴f (x)＝ax3＋cx 又当x＝－时，f (x)取得极大值
∴ 解得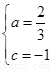
，∴f (x)＝x3－x，f¢ (x)＝2x2－1 …………6分
⑵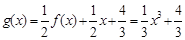
，设切点为
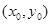，则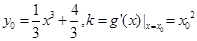
切线方程为：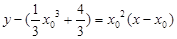
，…………………………………………8分
代入点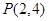
化简得：
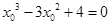，解得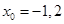
，……………………10分
所以切线方程为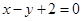：和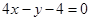。………………………………12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
