题目内容
定义全集U的子集A的特征函数为fA(x)=
,这里?UA表示集合A在全集U中的补集,已A⊆U,B⊆U,给出以下结论中不正确的是( )
|
分析:根据题中特征函数的定义,利用集合的交集、并集和补集运算法则,对A、B、C、D各项中的运算加以验证,可得A、B、C都可以证明它们的正确性,而D项可通过反例说明它不正确.由此得到本题答案.
解答:解:由题意,可得
对于A,因为A⊆B,可得x∈A则x∈B,
∵fA(x)=
,fB(x)=
,
而CUA中可能有B的元素,但CUB中不可能有A的元素
∴fA(x)≤fB(x),
即对于任意x∈U,都有fA(x)≤fB(x)故A正确;
对于B,因为f CUA=
,
结合fA(x)的表达式,可得f CUA=1-fA(x),故B正确;
对于C,fA∩B(x)=
=
=
•
=fA(x)•fB(x),
故C正确;
对于D,fA∪B(x)=
当某个元素x在A中但不在B中,由于它在A∪B中,故fA∪B(x)=1,
而fA(x)=1且fB(x)=0,可得fA∪B(x)≠fA(x)•fB(x)
由此可得D不正确.
故选:D
对于A,因为A⊆B,可得x∈A则x∈B,
∵fA(x)=
|
|
而CUA中可能有B的元素,但CUB中不可能有A的元素
∴fA(x)≤fB(x),
即对于任意x∈U,都有fA(x)≤fB(x)故A正确;
对于B,因为f CUA=
|
结合fA(x)的表达式,可得f CUA=1-fA(x),故B正确;
对于C,fA∩B(x)=
|
|
=
|
|
故C正确;
对于D,fA∪B(x)=
|
当某个元素x在A中但不在B中,由于它在A∪B中,故fA∪B(x)=1,
而fA(x)=1且fB(x)=0,可得fA∪B(x)≠fA(x)•fB(x)
由此可得D不正确.
故选:D
点评:本题给出特征函数的定义,判断几个命题的真假性,着重考查了集合的运算性质和函数对应法则的理解等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
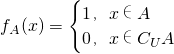 ,这里CUA表示A在全集U中的补集,那么对于集合A、B⊆U,下列所有正确说法的序号是______.
,这里CUA表示A在全集U中的补集,那么对于集合A、B⊆U,下列所有正确说法的序号是______. 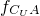 (x)=1-fA(x)
(x)=1-fA(x)