题目内容
对于函数y=f(x),若存在开区间D,同时满足:①存在t∈D,当x<t时,函数f(x)单调递减,当x>t时,函数f(x)单调递增;②对任意x>0,只要t-x,t+x∈D,都有f(t-x)>f(t+x),则称y=f(x)为D内的“勾函数”.
(1)证明:函数y=|logax|(a>0,a≠1)为(0,+∞)内的“勾函数”;
(2)若D内的“勾函数”y=g(x)的导函数为y=g′(x),y=g(x)在D内有两个零点x1,x2,求证: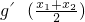 >0;
>0;
(3)对于给定常数λ,是否存在m,使函数h(x)= λx3-
λx3- λ2x2-2λ3x+1在(m,+∞)内为“勾函数”?若存在,试求出m的取值范围,若不存在,说明理由.
λ2x2-2λ3x+1在(m,+∞)内为“勾函数”?若存在,试求出m的取值范围,若不存在,说明理由.
解:(1)只证明0<a<1.
设0<a<1,则f(x)= ,
,
取t=1,则函数f(x)=logax在区间(0,1]上单调递减;f(x)=-logax在区间(1,+∞)上单调递增,因此满足条件①.
任取x∈(0,1),则1-x,(1+x)∈(0,+∞),而loga(1-x)-(-loga(1+x))=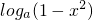 >0,即满足条件②.
>0,即满足条件②.
由以上证明可知:当0<a<1时,函数y=|logax|(1>a>0,a≠1)为(0,+∞)内的“勾函数”;
当a>1时,同理可证.
综上可知:函数y=|logax|(a>0,a≠1)为(0,+∞)内的“勾函数”;
(2)设勾函数y=g(x)的定义域为(a,+∞)(a>0),且g(x)在区间(a,t)单调递减;在区间(t,+∞)内单调递增;
因为存在两个零点,设g(x1)=g(x2)=0,不妨设x1<x2,由题意可得a<x1<t<x2,∴g(t-(t-x1))>g(t+t-x1),化为g(x1)>g(2t-x1),
∴g(x2)>g(2t-x1),
∵g(x)在区间(t,+∞)内单调递增,∴x2>2t-x1,∴ ,
,
∴ .
.
(3)h′(x)=λ(x-2λ)(x+λ),令h′(x)=0,解得x=2λ或-λ.
①当λ>0时,列表如下:
由表格可知:h(x)在区间(-λ,+∞)上满足“勾函数”的第一个条件;
但是当0<x<2λ时,h(2λ-x)-h(2λ+x)= <0,不满足“勾函数”的第二个条件.
<0,不满足“勾函数”的第二个条件.
因此此时函数h(x)表示“勾函数”.
②当λ<0时,不满足“勾函数”的第一个条件.
故不存在m使函数h(x)= λx3-
λx3- λ2x2-2λ3x+1在(m,+∞)内为“勾函数”.
λ2x2-2λ3x+1在(m,+∞)内为“勾函数”.
分析:(1)通过对底数a分类讨论,利用对数函数的单调性和“勾函数”的定义即可证明结论;
(2)利用“勾函数”的定义及已知条件即可证明;
(3)利用“勾函数”的定义中的两个条件判断是否满足即可.
点评:熟练掌握对数函数的单调性、“勾函数”的定义、利用导数研究函数的单调性是解题的关键.
设0<a<1,则f(x)=
 ,
,取t=1,则函数f(x)=logax在区间(0,1]上单调递减;f(x)=-logax在区间(1,+∞)上单调递增,因此满足条件①.
任取x∈(0,1),则1-x,(1+x)∈(0,+∞),而loga(1-x)-(-loga(1+x))=
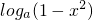 >0,即满足条件②.
>0,即满足条件②.由以上证明可知:当0<a<1时,函数y=|logax|(1>a>0,a≠1)为(0,+∞)内的“勾函数”;
当a>1时,同理可证.
综上可知:函数y=|logax|(a>0,a≠1)为(0,+∞)内的“勾函数”;
(2)设勾函数y=g(x)的定义域为(a,+∞)(a>0),且g(x)在区间(a,t)单调递减;在区间(t,+∞)内单调递增;
因为存在两个零点,设g(x1)=g(x2)=0,不妨设x1<x2,由题意可得a<x1<t<x2,∴g(t-(t-x1))>g(t+t-x1),化为g(x1)>g(2t-x1),
∴g(x2)>g(2t-x1),
∵g(x)在区间(t,+∞)内单调递增,∴x2>2t-x1,∴
 ,
,∴
 .
.(3)h′(x)=λ(x-2λ)(x+λ),令h′(x)=0,解得x=2λ或-λ.

①当λ>0时,列表如下:
由表格可知:h(x)在区间(-λ,+∞)上满足“勾函数”的第一个条件;
但是当0<x<2λ时,h(2λ-x)-h(2λ+x)=
 <0,不满足“勾函数”的第二个条件.
<0,不满足“勾函数”的第二个条件.因此此时函数h(x)表示“勾函数”.
②当λ<0时,不满足“勾函数”的第一个条件.
故不存在m使函数h(x)=
 λx3-
λx3- λ2x2-2λ3x+1在(m,+∞)内为“勾函数”.
λ2x2-2λ3x+1在(m,+∞)内为“勾函数”.分析:(1)通过对底数a分类讨论,利用对数函数的单调性和“勾函数”的定义即可证明结论;
(2)利用“勾函数”的定义及已知条件即可证明;
(3)利用“勾函数”的定义中的两个条件判断是否满足即可.
点评:熟练掌握对数函数的单调性、“勾函数”的定义、利用导数研究函数的单调性是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目