题目内容
设数列{an}(n=1,2,…)是等差数列,且公差为d,若数列{an}中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
(1)若a1=4,d=2,求证:该数列是“封闭数列”;
(2)试判断数列an=2n-7(n∈N*)是否是“封闭数列”,为什么?
(3)设Sn是数列{an}的前n项和,若公差d=1,a1>0,试问:是否存在这样的“封闭数列”,使![]() ;若存在,求{an}的通项公式,若不存在,说明理由.
;若存在,求{an}的通项公式,若不存在,说明理由.
答案:
解析:
解析:
|
(1)证明: 对任意的 ∵m+n+1∈N*于是,令 (2) 令 所以数列 (3)解:由 于是有 若 若 若 综上所述, |

练习册系列答案
相关题目
 ,14分
,14分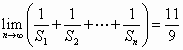 ,16分
,16分 ,17分
,17分