题目内容
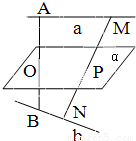
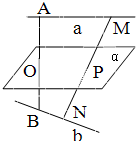已知异面直线a，b的公垂线段AB的中点为O，平面α满足a∥α，b∥α，且O∈α，M、N是a，b上的任意两点，MN∩α=P，求证：P是MN的中点．分析：如图所示，连接AN交平面 α 于Q，连接OQ、PQ，利用线面平行的性质定理和判定定理即三角形的中位线定理即可证明．
解答：证明：连接AN交平面 α 于Q，连接OQ、PQ，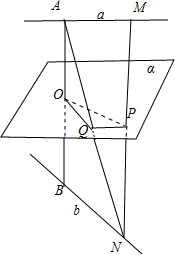
∵A∉b，∴A、b可确定平面β，
∴α∩β=OQ，由b∥α 得 BN∥OQ．
∵O为AB的中点，∴Q为AN的中点．
同理 PQ∥AM，故 P为MN的中点．
∵A∉b，∴A、b可确定平面β，
∴α∩β=OQ，由b∥α 得 BN∥OQ．
∵O为AB的中点，∴Q为AN的中点．
同理 PQ∥AM，故 P为MN的中点．
点评：熟练掌握线面平行的判定定理和性质定理是解题的关键．
练习册系列答案
新思维寒假作业系列答案
相关题目
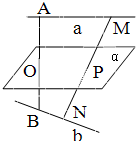已知异面直线a，b的公垂线段AB的中点为O，平面α满足a∥α，b∥α，且O∈α，M、N是a，b上的任意两点，MN∩α=P，求证：P是MN的中点．
