题目内容
数列![]() 中,
中,![]() ;
;![]() , 对任意的
, 对任意的![]() 为正整数都有
为正整数都有![]() 。
。
(1)求证:![]() 是等差数列;
是等差数列;
(2)求出![]()
![]() 的通项公式
的通项公式![]() ;
;
(3)若![]() (
(![]() ),是否存在实数
),是否存在实数![]() 使得
使得![]() 对任意的
对任意的![]() 恒成立?若存在,找出
恒成立?若存在,找出![]() ;若不存在,请说明理由。
;若不存在,请说明理由。
解:(1)由题意可知![]()
![]()
![]() (
(![]() )两式相减可得
)两式相减可得![]()
![]() ,又
,又![]()
![]() 也成立,所以
也成立,所以![]() ,
,![]() ,等式两边同乘
,等式两边同乘![]() 可得
可得
![]() ,所以
,所以![]()
所以![]() 是等差数列。…………………6分
是等差数列。…………………6分
(2)![]() ,
,![]() ,所以
,所以![]()
![]() (
(![]() ) ………………8分
) ………………8分
(3)![]() ,
,![]()
两式相减可得![]()
所以![]() (
(![]() )
)
所以![]()
各项为![]()
![]() 恒成立,所以上述数列中奇数项从
恒成立,所以上述数列中奇数项从![]() 递增趋向于零,偶数项从
递增趋向于零,偶数项从![]() 递减趋向于零,所以存在
递减趋向于零,所以存在![]() 使得
使得![]() 对任意的
对任意的![]() 恒成立。…………………14分
恒成立。…………………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
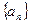 中,
中,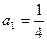 ;
;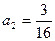 ,对任意的
,对任意的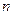 为正整数都有
为正整数都有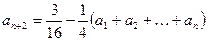 。
。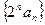 是等差数列;
是等差数列;
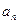 ;
;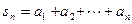 (
(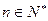 ),是否存在实数
),是否存在实数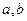 使得
使得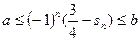 对任意的
对任意的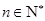 ,数列
,数列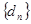 满足
满足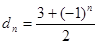 ,数列
,数列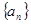 满足
满足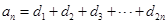 ;又知数列
;又知数列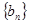 中,
中,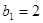 ,且对任意正整数
,且对任意正整数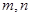 ,
,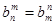 .
.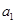 项,第
项,第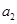 项,第
项,第 项,……,第
项,……,第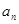 项,……删去后,剩余的项按从小到大的顺序排成新数列
项,……删去后,剩余的项按从小到大的顺序排成新数列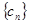 ,求数列
,求数列 项和.
项和.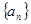 中,
中,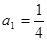 ;
;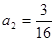 , 对任意的
, 对任意的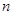 为正整数都有
为正整数都有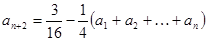 。
。 是等差数列;
是等差数列;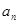 ;
;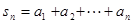 (
(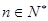 ),是否存在实数
),是否存在实数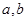 使得
使得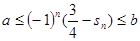 对任意的
对任意的 中,
中, ,且对任意
,且对任意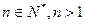 都有
都有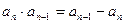 成立,令
成立,令 (1)求数列
(1)求数列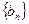 的通项公式;(2)求数列
的通项公式;(2)求数列 的前n项和
的前n项和 。
。