题目内容
 设不等式组
设不等式组 确定的平面区域为U,
确定的平面区域为U, 确定的平面区域为V.
确定的平面区域为V.
(I)定义坐标为整数的点为“整点”.在区域U内任取3个整点,求这些整点中恰有2个整点在区域V的概率;
(II)在区域U内任取3个点,记此3个点在区域V的个数为X,求X的概率分布列及其数学期望.
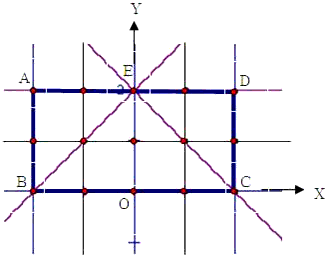 解:(Ⅰ)由题意,区域U内共有15个整点,区域V内共有9个整点,
解:(Ⅰ)由题意,区域U内共有15个整点,区域V内共有9个整点,设所取3个整点中恰有2个整点在区域V的概率为P(v),
则P(v)=
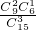 =
= .
. (Ⅱ)区域U的面积为8,区域V的面积为4,
∴在区域U内任取一点,该点在区域V内的概率为
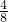 =
= .
. 则X的取值为0,1,2,3,
P(X=0)=C30(
 )0(
)0( )3=
)3= ,
,P(X=1)=C31(
 )1(
)1( )2=
)2= ,
,P(X=0)=C32(
 )2(
)2( )1=
)1= ,
,P(X=3)=C33(
 )3(
)3( )0=
)0= ,
,∴X的分布列为
| X | 0 | 1 | 2 | 3 |
| P(X) |  |  |  |  |
 +1×
+1× +2×
+2× +3×
+3× =
=
分析:(Ⅰ)根据题意,画出区域U与V,可得其中整点的个数,进而由古典概型公式,计算可得答案;
(Ⅱ)根据题意,易得区域U的面积为8,区域V的面积为4,进而可得在区域U内任取一点,该点在区域V内的概率,依题意可得X的取值为0,1,2,3;由n次独立重复试验中恰有k次发生的概率公式,可得X为0,1,2,3的概率,可得X的分布列,进而由期望公式,计算可得答案.
点评:本题考查排列组合的运用、离散型变量的期望与方差的计算,解题时注意(Ⅰ)涉及整点,是古典概型;(Ⅱ)利用面积,是几何概型.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 设不等式组
设不等式组 设不等式组
设不等式组 确定的平面区域为U,
确定的平面区域为U, 确定的平面区域为V.
确定的平面区域为V.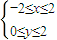 确定的平面区域为U,
确定的平面区域为U,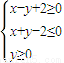 确定的平面区域为V.
确定的平面区域为V.
 设不等式组
设不等式组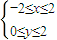 确定的平面区域为U,
确定的平面区域为U,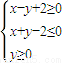 确定的平面区域为V.
确定的平面区域为V.