题目内容
某校为了解高一学生英语学习的情况,现从期末英语考试成绩中随机抽取100名学生,按成绩分组,得到的频率分布表如图:| 组别 | 分组 | 组数 | 频率 |
| 1 | [90,100﹚ | 3 | 0.03 |
| 2 | [100,110﹚ | 30 | 0.3 |
| 3 | [110,120﹚ | 10 | ① |
| 4 | [120,130﹚ | ② | 0.34 |
| 5 | [130,140﹚ | 21 | 0.21 |
| 6 | [140,150﹚ | 2 | 1 |
| 合计 | 100 | 1 |
(2)若在第3、5组的学生中,用分层抽样抽取6名学生参加心理测试,请问:在第3、5组各抽取多少名学生参加测试;
(3)为了进一步获得研究资料,学校决定再从第1组和第6组的学生中,随机抽取3名学生进行心理测试,列出所有基本事件,并求㈠第1组中的甲同学和第6组中的A同学都没有被抽到的概率;㈡第1组中至少有两个同学入选的概率.
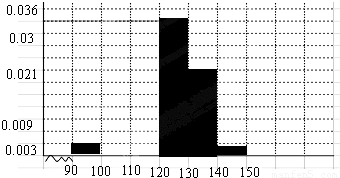
【答案】分析:题干错误:频率列的倒数第二行不应该为1,应该是0.02,请给修改,谢谢.
(1)在频率分布表中,①为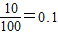 ,②为0.34×100=34,频率分布直方图如图所示.
,②为0.34×100=34,频率分布直方图如图所示.
(2)样本容量为31人,按照分层抽样比例,求得第三组中应该抽取的人数,在第五组中应该抽取的人数.
(3)设第一组的三个人分别为甲、乙、丙,第六组的2个人分别为A、B,随机抽取3名学生进行心理测试,列出所有基本事件,共计10个基本事件.
(一)第1组中的甲同学和第6组中的A同学都没有被抽到的方法有一种,所有的抽法有10种,由此求得所求事件的概率为概率.
(二)第1组中至少有两个同学入选的抽法共有7种,所有的抽法有10种,由此求得所求事件的概率.
解答:解:(1)①②依题意可得:在频率分布表中,①为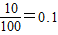 ;…(1分)
;…(1分)
②为0.34×100=34.…(2分)
频率分布直方图如图:--(3分)
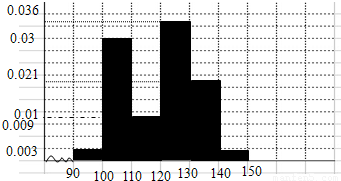
(2)样本容量为31人,按照分层抽样比例,在第三组中应该抽取2人,在第五组中应该抽取4人参加测试.…(6分)
(3)设第一组的三个人分别为甲、乙、丙,第六组的2个人分别为A、B,随机抽取3名学生进行心理测试,列出所有基本事件为:
(甲,乙,丙)、(甲,乙,A)、(甲,乙,B)、(甲,丙,A)、(甲,丙,B)、(乙,丙,A)、(乙,丙,B)、
(甲,A,B)、(乙,A,B)、(丙,A,B),共计10个基本事件.
(一)第1组中的甲同学和第6组中的A同学都没有被抽到的方法有一种,所有的抽法有10种,故所求事件的概率为概率为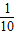 .
.
㈡第1组中至少有两个同学入选的抽法共有7种,所有的抽法有10种,故所求事件的概率为概率为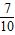 .
.
点评:本题主要考查分层抽样的定义和方法,频率分步表、频率分布直方图的应用,古典概型及其概率计算公式的应用,属于基础题.
(1)在频率分布表中,①为
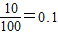 ,②为0.34×100=34,频率分布直方图如图所示.
,②为0.34×100=34,频率分布直方图如图所示.(2)样本容量为31人,按照分层抽样比例,求得第三组中应该抽取的人数,在第五组中应该抽取的人数.
(3)设第一组的三个人分别为甲、乙、丙,第六组的2个人分别为A、B,随机抽取3名学生进行心理测试,列出所有基本事件,共计10个基本事件.
(一)第1组中的甲同学和第6组中的A同学都没有被抽到的方法有一种,所有的抽法有10种,由此求得所求事件的概率为概率.
(二)第1组中至少有两个同学入选的抽法共有7种,所有的抽法有10种,由此求得所求事件的概率.
解答:解:(1)①②依题意可得:在频率分布表中,①为
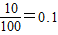 ;…(1分)
;…(1分)②为0.34×100=34.…(2分)
频率分布直方图如图:--(3分)

(2)样本容量为31人,按照分层抽样比例,在第三组中应该抽取2人,在第五组中应该抽取4人参加测试.…(6分)
(3)设第一组的三个人分别为甲、乙、丙,第六组的2个人分别为A、B,随机抽取3名学生进行心理测试,列出所有基本事件为:
(甲,乙,丙)、(甲,乙,A)、(甲,乙,B)、(甲,丙,A)、(甲,丙,B)、(乙,丙,A)、(乙,丙,B)、
(甲,A,B)、(乙,A,B)、(丙,A,B),共计10个基本事件.
(一)第1组中的甲同学和第6组中的A同学都没有被抽到的方法有一种,所有的抽法有10种,故所求事件的概率为概率为
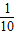 .
.㈡第1组中至少有两个同学入选的抽法共有7种,所有的抽法有10种,故所求事件的概率为概率为
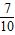 .
.点评:本题主要考查分层抽样的定义和方法,频率分步表、频率分布直方图的应用,古典概型及其概率计算公式的应用,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
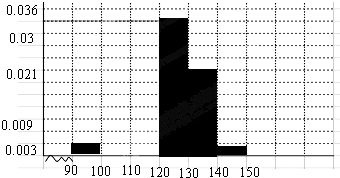 某校为了解高一学生英语学习的情况,现从期末英语考试成绩中随机抽取100名学生,按成绩分组,得到的频率分布表如图:
某校为了解高一学生英语学习的情况,现从期末英语考试成绩中随机抽取100名学生,按成绩分组,得到的频率分布表如图: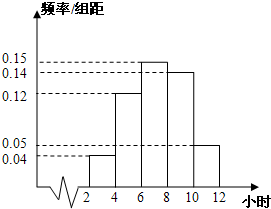 某校为了解高一学生寒假期间的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率分布直方图(如图所示),那么这100名学生中阅读时间在[4,8)小时内的人数为
某校为了解高一学生寒假期间的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率分布直方图(如图所示),那么这100名学生中阅读时间在[4,8)小时内的人数为