题目内容
(1)不等式2|x|+|x-1|<2的解集是(2)在极坐标系中,过点(2
 ,
, 作圆ρ=4sinθ的切线,则切线的极坐标方程为 .
作圆ρ=4sinθ的切线,则切线的极坐标方程为 .
【答案】分析:(1)把要求的不等式化为① ,或 ②
,或 ② ,或 ③
,或 ③ ,分别求出①②③的解集,取并集即得所求.
,分别求出①②③的解集,取并集即得所求.
(2)求出切线经过的点的直角坐标,再求出圆的直角坐标方程,求出圆的切线方程,再化为极坐标方程.
解答:解:(1)由不等式2|x|+|x-1|<2可得① ,或 ②
,或 ② ,或 ③
,或 ③ .
.
解①得- <x<0,解②得0≤x<1,解③得 x∈∅.
<x<0,解②得0≤x<1,解③得 x∈∅.
故不等式的解集为(- ,1),
,1),
故答案为 (- ,1).
,1).
(2)点(2 ,
, 的直角坐标为(2,2),圆ρ=4sinθ 即 ρ2=4ρsinθ,化简可得 x2+(y-2)2=4,表示以(0,2)为圆心、以2为半径的圆.
的直角坐标为(2,2),圆ρ=4sinθ 即 ρ2=4ρsinθ,化简可得 x2+(y-2)2=4,表示以(0,2)为圆心、以2为半径的圆.
由题意可得,圆的切线斜率不存在,故切线方程为 x=2,化为极坐标方程为ρcosθ=2,
故答案为 ρcosθ=2.
点评:本题主要考查绝对值不等式的解法,极坐标方程与直角坐标方程的互化,求圆的切线方程,体现了分类讨论的数学思想,属于中档题.
 ,或 ②
,或 ② ,或 ③
,或 ③ ,分别求出①②③的解集,取并集即得所求.
,分别求出①②③的解集,取并集即得所求.(2)求出切线经过的点的直角坐标,再求出圆的直角坐标方程,求出圆的切线方程,再化为极坐标方程.
解答:解:(1)由不等式2|x|+|x-1|<2可得①
 ,或 ②
,或 ② ,或 ③
,或 ③ .
.解①得-
 <x<0,解②得0≤x<1,解③得 x∈∅.
<x<0,解②得0≤x<1,解③得 x∈∅.故不等式的解集为(-
 ,1),
,1),故答案为 (-
 ,1).
,1).(2)点(2
 ,
, 的直角坐标为(2,2),圆ρ=4sinθ 即 ρ2=4ρsinθ,化简可得 x2+(y-2)2=4,表示以(0,2)为圆心、以2为半径的圆.
的直角坐标为(2,2),圆ρ=4sinθ 即 ρ2=4ρsinθ,化简可得 x2+(y-2)2=4,表示以(0,2)为圆心、以2为半径的圆.由题意可得,圆的切线斜率不存在,故切线方程为 x=2,化为极坐标方程为ρcosθ=2,
故答案为 ρcosθ=2.
点评:本题主要考查绝对值不等式的解法,极坐标方程与直角坐标方程的互化,求圆的切线方程,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 ,
,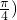 作圆ρ=4sinθ的切线,则切线的极坐标方程为________.
作圆ρ=4sinθ的切线,则切线的极坐标方程为________.